درک مرتبسازی حبابی: روش مرتبسازی ساده

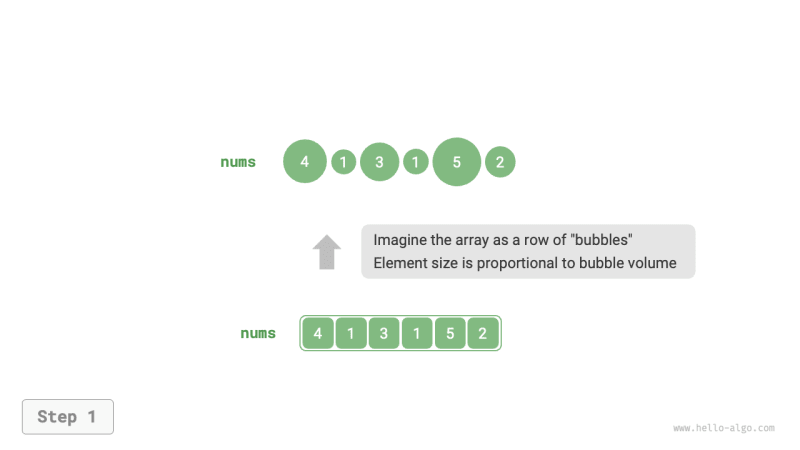
مرتب سازی حبابی مرتب سازی را با مقایسه و مبادله مداوم عناصر مجاور انجام می دهد. این فرآیند شبیه حباب هایی است که از پایین به بالا بالا می روند، از این رو به آن مرتب سازی حبابی می گویند.
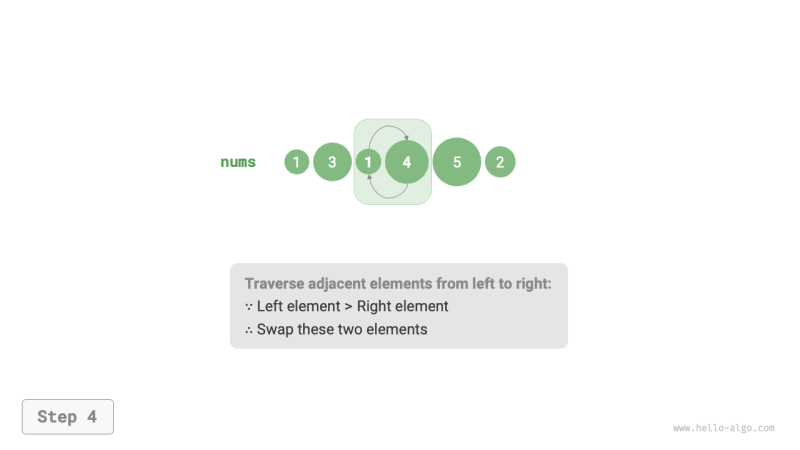
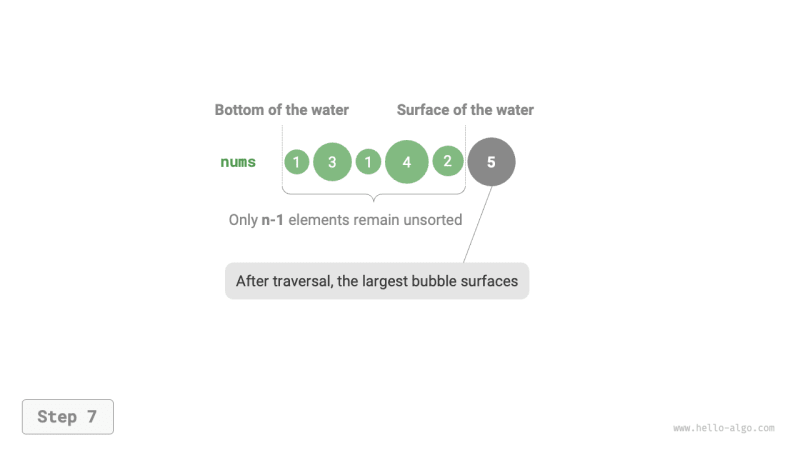
همانطور که در شکل زیر نشان داده شده است، فرآیند حباب را می توان با استفاده از عملیات تعویض عنصر شبیه سازی کرد: با شروع از سمت چپ ترین انتهای آرایه و حرکت به سمت راست، اندازه عناصر مجاور را به ترتیب مقایسه کنید. اگر “عنصر چپ > عنصر سمت راست”، آنها را عوض کنید. پس از پیمایش، بزرگترین عنصر به انتهای سمت راست آرایه منتقل می شود.
=== “”
=== “”
=== “”
=== “”
=== “”
=== “”
=== “”
فرآیند الگوریتم
با فرض اینکه طول آرایه $n$ باشد، مراحل مرتب سازی حبابی در شکل زیر نشان داده شده است.
- ابتدا یک “حباب” روی عناصر $n$ انجام دهید، جابجایی بزرگترین عنصر در موقعیت صحیح خود.
- سپس، یک “حباب” را روی عناصر باقیمانده $n – 1$ انجام دهید. تعویض دومین عنصر بزرگ در موقعیت صحیح خود.
- به طور مشابه، پس از $n – 1$ دور “حباب”، بزرگترین عناصر بالای $n – 1$ به موقعیت های صحیح خود مبادله می شوند.
- تنها عنصر باقی مانده لزوما کوچکترین است و نیازی به مرتب سازی ندارد، بنابراین مرتب سازی آرایه کامل است.

بهینه سازی کارایی
متوجه میشویم که اگر هیچ تعویضی در یک دور «حبابسازی» انجام نشود، آرایه از قبل مرتب شده است و میتوانیم بلافاصله نتیجه را برگردانیم. بنابراین، ما می توانیم یک پرچم اضافه کنیم flag برای نظارت بر این وضعیت و بلافاصله پس از وقوع آن بازگشت.
حتی پس از بهینهسازی، پیچیدگی زمانی در بدترین حالت و میانگین پیچیدگی زمانی مرتبسازی حبابی در $O(n^2)$ باقی میماند. با این حال، زمانی که آرایه ورودی به طور کامل مرتب شود، می تواند به بهترین پیچیدگی زمانی $O(n)$ دست یابد.
کد جاوا –
public class BubbleSort {
public int[] sortArray(int[] nums) {
for (int i = nums.length - 1; i > 0; i--) {
boolean flag = false;
for (int j = 0; j i; j++) {
if (nums[j] > nums[j + 1]) {
int tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
flag = true;
}
}
if (!flag) {
break;
}
}
return nums;
}
}
کد پایتون –
def bubbleSort(nums):
for i in range(len(nums)-1,0,-1):
flag=False;
for j in range(i):
if nums[j]>nums[j+1]:
nums[j],nums[j+1]=nums[j+1],nums[j];
flag=True;
if not flag:
break;
return nums;
ویژگی های الگوریتم
-
پیچیدگی زمانی $O(n^2)$، مرتبسازی تطبیقی: طول آرایه پیموده شده در هر دور “حباب” به ترتیب از $n – 1$، $n – 2$، $\dots$، $2$، $1$ کاهش مییابد که در مجموع $(n – 1) n / 2 است. $. با معرفی
flagبهینه سازی، بهترین پیچیدگی زمانی می تواند به $O(n)$ برسد. - پیچیدگی فضایی $O(1)$، مرتبسازی در محل: فقط مقدار ثابتی از فضای اضافی توسط نشانگرهای $i$ و $j$ استفاده می شود.
- مرتب سازی پایدار: به عنوان عناصر مساوی در طول “حباب” مبادله نمی شود.
مرجع :-



