چگونه می توان پادشاهی Henbane را دریافت کرد: تحویل 2

مناظر پادشاهی بیا: تحویل 2 غنی از گیاهان و گیاهان هستند که بسیاری از آنها هدف فراتر از مناظر را ارائه می دهند. این مواد تشکیل دهنده برای تولید معجون هایی که می توانند بهبود بخشیده ، توانایی های شما را تقویت کنند ، یا حتی برای ناتوانی دشمنان نیز ضروری هستند.
مربوط
اگر می خواهید یک معجون خاص را تهیه کنید اما در تلاش برای یافتن یک ماده اصلی هستید ، می تواند ناامید کننده باشد زیرا بازی همیشه جهت های روشنی را ارائه نمی دهد. یکی از این گیاه ها Henbane است. در حالی که گاهی اوقات می توانید آن را در طبیعت پیدا کنید ، قابل اطمینان ترین راه برای به دست آوردن آن با خرید آن از گیاه شناس است. اگر تعجب می کنید که از کجا می توانید دست خود را به دست بیاورید ، این راهنما شما را پوشش داده است.
چگونه Henbane را بدست آوریم
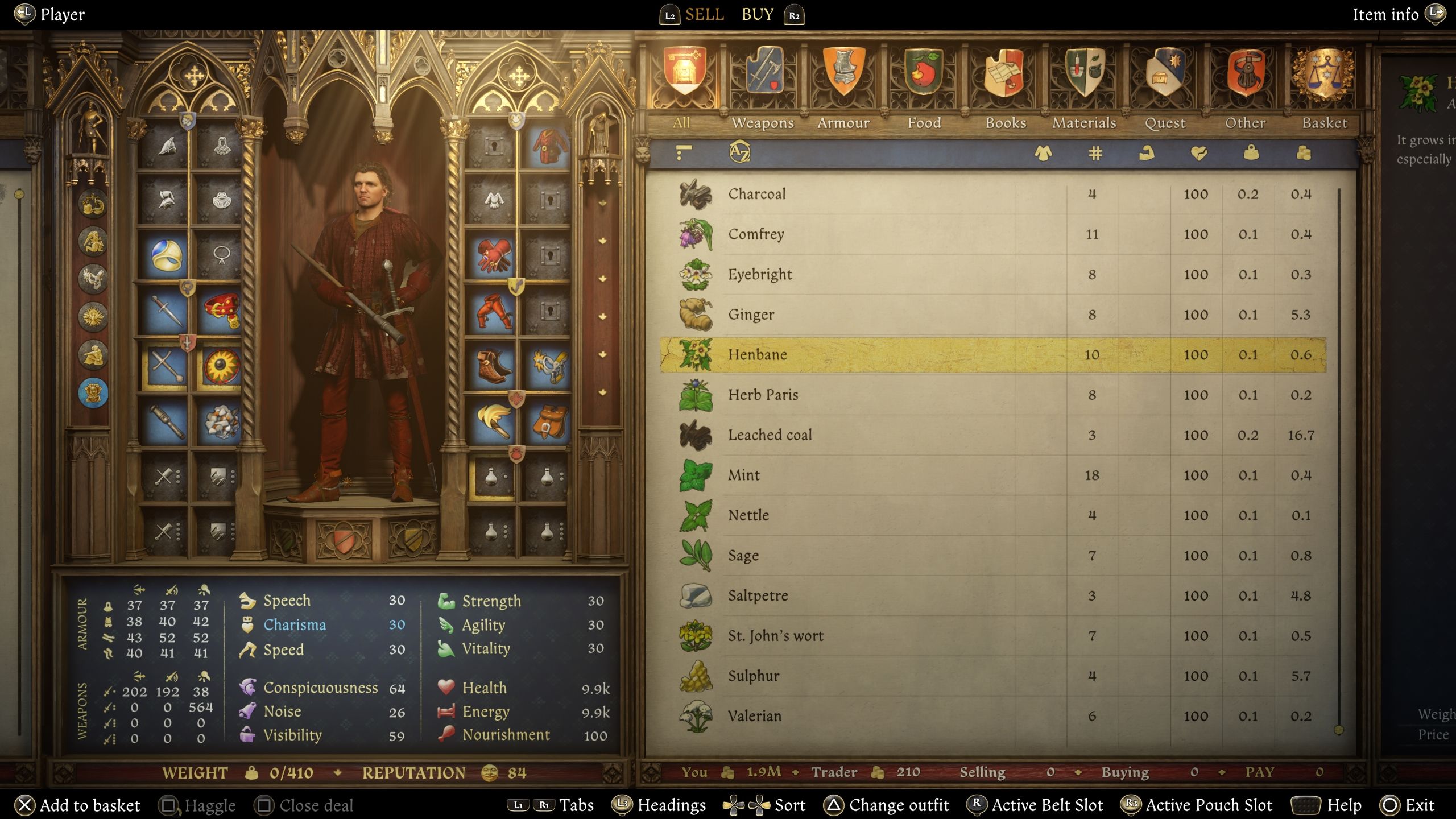
سنبل یک ماده کیمیاگری مسموم است که می توانید در دنیای آزاد پیدا کنید یا خرید از بازرگانان خاص.
Henbane یک است گیاه سبز متمایز با گلهای زرد مایل به زرد و ساقه های برگ دار و برگ داربشر معمولاً از نظر اندازه کوچکتر است و در مزارع و زمین حاصلخیز یافت می شود. این گیاه عمدتاً برای ساخت معجون های مسموم استفاده می شود.
در حال حاضر ، ما فقط راه های خرید Henbane را به جای پیدا کردن آن در طبیعت تأیید کرده ایمبشر خوشبختانه ، ارزان است ، بنابراین به دست آوردن آن نباید مسئله ای باشد.
-
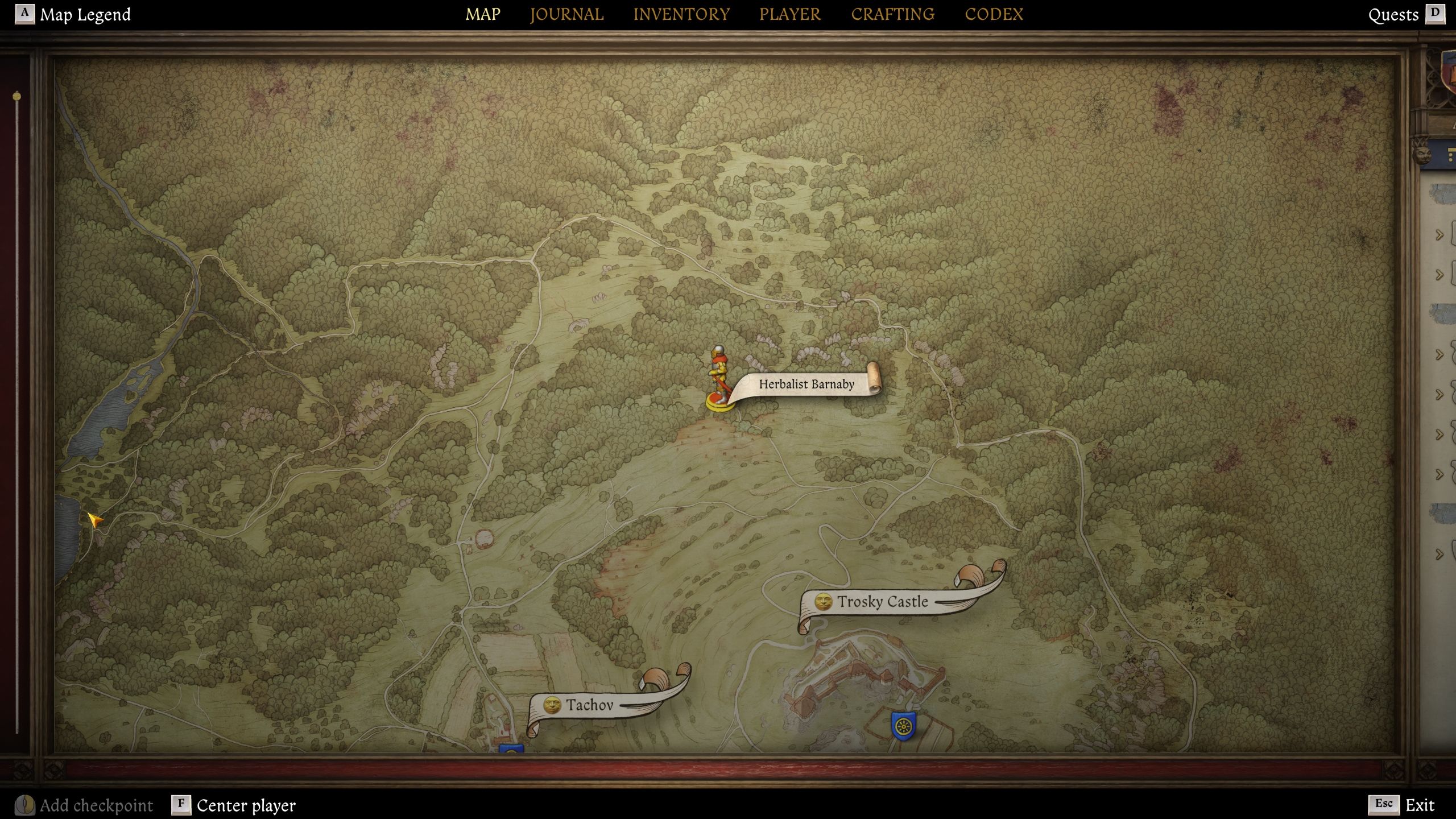
اولین مکان برای خرید Henbane از آن است برنابی گیاهی، چه کسی را می توان پیدا کرد در شمال دور قلعه Trosky در یک خانه کوچک و جداگانه.
-
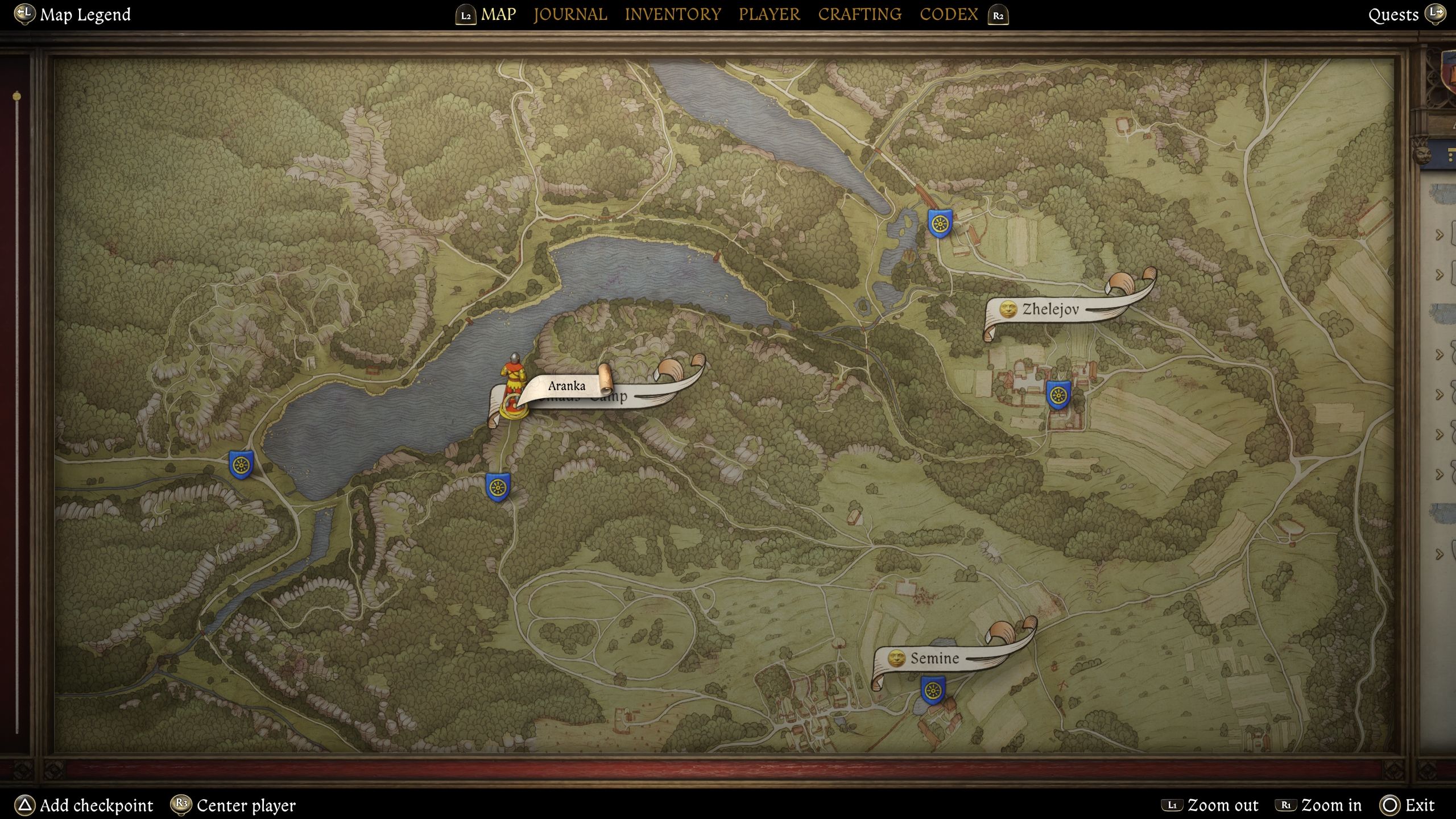
مکان دوم است گیاه شناس آوانکا، واقع در غرب نقشه در اردوگاه عشایر، جایی که او را می توان در چادر خود پیدا کرد.
-
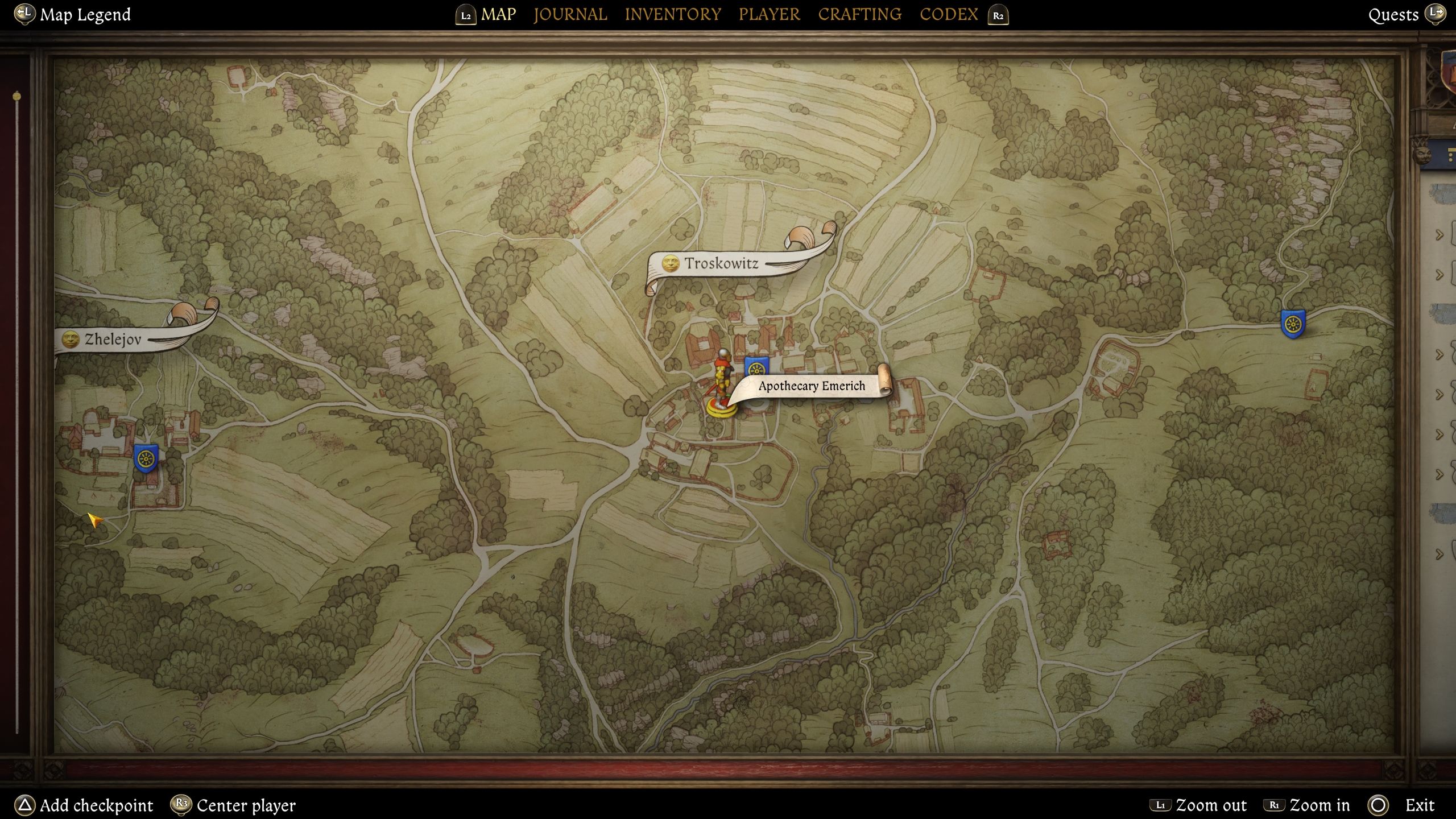
گزینه سوم است امری، که فقط واقع شده است جنوب غربی نقطه سفر سریع در شهر Troskowitzبشر او نسخه خشک Henbane را به فروش می رساند ، که از نظر عملکردی یکسان است.
-
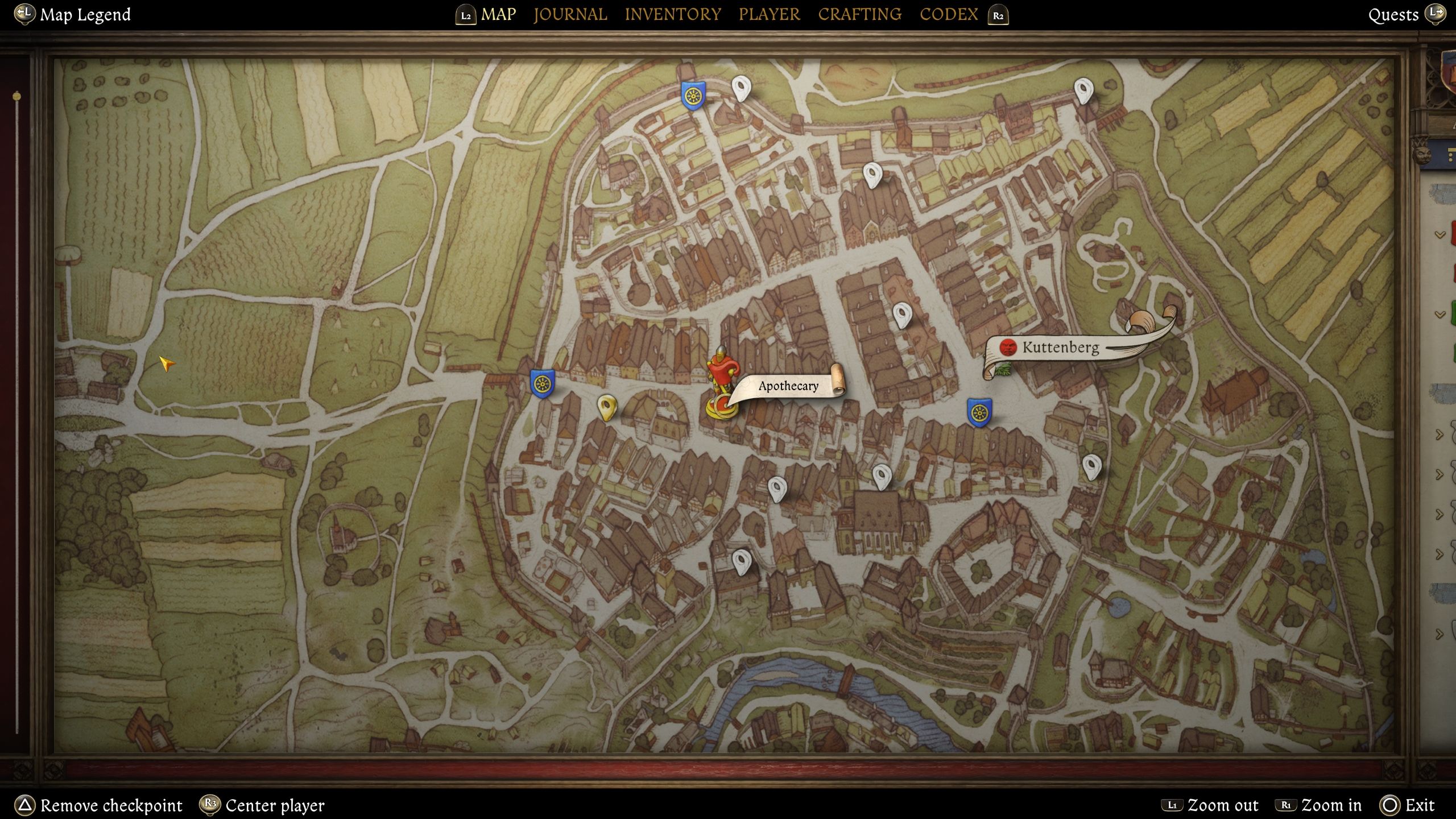
مکان چهارم و نهایی Apothecary در غرب چشمه در منطقه Kuttenbergبشر او مانند Emmerich ، نسخه خشک را نیز به فروش می رساند.
ممکن است شما در دنیای آزاد با Henbane روبرو شوید ، اما با وجود فروشندگان متعدد ، آن را با قیمت پایین ارائه می دهند ، اغلب سفر سریع به یکی از مکان های آنها و خرید آن ساده تر است.

طرف دیگر
پادشاهی بیا: تحویل 2 – چگونه بابونه
در اینجا آمده است که چگونه می توانید در Kingdom Come باب بابونه دریافت کنید: تحویل 2.