1092. کوتاهترین صعود مشترک – جامعه dev

1092 کوتاهترین صعود مشترک

مشکل: سخت

مباحث: Stringبا Dynamic Programming

با توجه به دو رشته str1 وت str2، بازگشت کوتاهترین رشته ای که هر دو دارد str1 وت str2 به عنوان پی در پیبشر اگر چندین رشته معتبر وجود دارد ، برگردید هیچ از آنها

یک رشته s پیروی از رشته است t در صورت حذف تعدادی از شخصیت ها t (احتمالاً 0) در رشته نتایج حاصل می شود sبشر

مثال 1:

• ورودی: str1 = “abac” ، str2 = “cab”
• خروجی: “کاباک”
• توضیح:
  • STR1 = “ABAC” متعاقباً “CABAC” است زیرا می توانیم اولین “C” را حذف کنیم.
  • STR2 = “CAB” متعاقباً “CABAC” است زیرا می توانیم آخرین “AC” را حذف کنیم.
  • پاسخ ارائه شده کوتاهترین رشته ای است که این خصوصیات را برآورده می کند.

مثال 2:

• ورودی: str1 = “aaaaaaaa” ، str2 = “aaaaaaaa”
• خروجی: “aaaaaaaaa”

محدودیت ها:

• 1 <= str1.length, str2.length <= 1000
• str1 وت str2 شامل حروف انگلیسی کوچک است.

نکته:

1. ما می توانیم طول طولانی ترین دنباله مشترک بین str1[i:] وت str2[j:] (برای همه (i, j)) با استفاده از برنامه نویسی پویا.
2. ما می توانیم از این اطلاعات برای بازیابی کوتاهترین صعود مشترک استفاده کنیم.

راه حل:

ما باید کوتاهترین صعود مشترک (SCS) دو رشته داده شده را پیدا کنیم. SCS کوتاهترین رشته ای است که شامل هر دو رشته ورودی به عنوان دنبال کننده است. این رویکرد شامل استفاده از برنامه نویسی پویا (DP) برای تعیین طولانی ترین دنباله مشترک (LCS) و سپس ساخت SCS با ادغام دو رشته ورودی بر اساس LCS است.

رویکرد

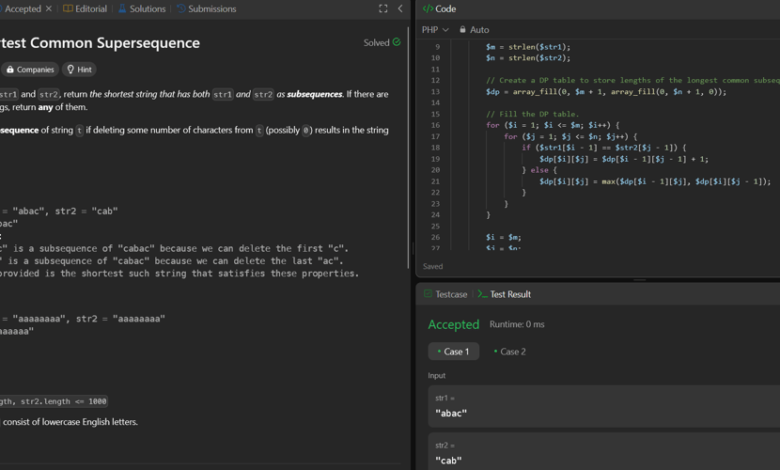
1. برنامه نویسی پویا (DP) ساخت جدول:

   • یک میز DP ایجاد کنید که در آن dp[i][j] طول LCS بستر ها را نشان می دهد str1[0..i-1] وت str2[0..j-1]بشر
   • جدول DP را با مقایسه کاراکترهای دو رشته و استفاده از مقادیر محاسبه شده قبلی برای ساخت راه حل پر کنید.

2. عقب نشینی برای ساخت SCS:

   • از جدول DP برای استفاده مجدد استفاده کنید dp[m][n] (کجا m وت n طول دو رشته) برای ساخت SCS است.
   • در حالی که در حال برگشت است ، شخصیت ها را از هر دو اضافه کنید str1 یا str2 بر اساس جهت حرکت در جدول DP. اگر شخصیت ها مطابقت داشته باشند ، آنها بخشی از LCS هستند و فقط یک بار اضافه می شوند. اگر آنها مطابقت ندارند ، در جهت مقدار DP بزرگتر حرکت کنید و شخصیت مربوطه را ضمیمه کنید.

3. دست زدن به شخصیت های باقی مانده:

   • پس از عقب نشینی ، هر نوع شخصیت باقیمانده را از هر رشته ای که در مرحله برگشت به عقب پردازش نشده است ، اضافه کنید.

4. نتیجه را معکوس کنید:

   • از آنجا که کاراکترها در حین بازگشت به صورت معکوس جمع آوری می شوند ، نتیجه را معکوس می کنند تا ترتیب صحیح SCS را بدست آورند.

بیایید این راه حل را در PHP پیاده سازی کنیم: 1092 کوتاهترین صعود مشترک

/**
 * @param String $str1
 * @param String $str2
 * @return String
 */
function shortestCommonSupersequence($str1, $str2) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example Cases
echo shortestCommonSupersequence("abac", "cab") . "\n";  // Output: "cabac"
echo shortestCommonSupersequence("aaaaaaaa", "aaaaaaaa") . "\n";  // Output: "aaaaaaaa"
?>

توضیح:

1. ساخت میز DP: جدول DP با مقایسه هر شخصیت از دو رشته ساخته شده است. اگر کاراکترها مطابقت داشته باشند ، مقدار از سلول مورب افزایش می یابد. اگر آنها مطابقت نداشته باشند ، مقدار از حداکثر سلول چپ یا فوقانی گرفته می شود.

2. پس انداز: با شروع از پایان هر دو رشته ، شخصیت ها بر اساس حضور آنها در LCS به نتیجه اضافه می شوند. اگر شخصیت ها مطابقت دارند ، یک بار اضافه می شوند. اگر اینگونه نباشد ، جهت با مقدار DP بالاتر انتخاب می شود و شخصیت مربوطه اضافه می شود.

3. دست زدن به شخصیت های باقی مانده: پس از حلقه اصلی ، هر شخصیت باقیمانده از هر رشته ضمیمه می شود تا اطمینان حاصل شود که همه شخصیت ها در SCS گنجانده شده اند.

4. معکوس کردن نتیجه: شخصیت های جمع آوری شده برای شکل دادن به ترتیب صحیح SCS معکوس می شوند.

این رویکرد با استفاده از LCS ، کوتاهترین صعود مشترک را ایجاد می کند و اطمینان حاصل می کند که راه حل هم بهینه و هم صحیح است.

پیوندهای تماس

اگر این سریال را مفید دیدید ، لطفاً در نظر بگیرید مخزن یک ستاره در GitHub یا به اشتراک گذاری پست در شبکه های اجتماعی مورد علاقه خود. حمایت شما برای من بسیار معنی دارد!

اگر می خواهید مطالب مفید تری مانند این ، احساس راحتی کنید که از من پیروی کنید: