2058. حداقل و حداکثر تعداد گره ها را بین نقاط بحرانی بیابید.

Summarize this content to 400 words in Persian Lang
2058. حداقل و حداکثر تعداد گره ها را بین نقاط بحرانی بیابید.

متوسط

آ نقطه بحرانی در یک لیست پیوندی به عنوان تعریف می شود یا آ حداکثر محلی یا الف حداقل های محلی.

یک گره یک است حداکثر محلی اگر گره فعلی یک مقدار داشته باشد به شدت بزرگتر نسبت به گره قبلی و گره بعدی.

یک گره یک است حداقل های محلی اگر گره فعلی یک مقدار داشته باشد به شدت کوچکتر نسبت به گره قبلی و گره بعدی.

توجه داشته باشید که یک گره تنها در صورت وجود می تواند حداکثر/حداقل محلی باشد هر دو یک گره قبلی و یک گره بعدی.

با توجه به یک لیست پیوندی head، برگشت آرایه ای به طول 2 شامل [minDistance, maxDistance] جایی که minDistance هست حداقل فاصله بین هر دو متمایز نقاط بحرانی و maxDistance هست حداکثر فاصله بین هر دو متمایز نقاط بحرانی. اگر وجود دارد کمتر از دو نقطه بحرانی، بازگشت [-1, -1].

مثال 1:

ورودی: سر = [3,1]

خروجی: [-1,-1]

توضیح: هیچ نقطه بحرانی در آن وجود ندارد [3,1].

مثال 2:

ورودی: سر = [5,3,1,2,5,1,2]

خروجی: [1,3]

توضیح: سه نکته مهم وجود دارد:

مثال 3:

ورودی: سر = [1,3,2,2,3,2,2,2,7]

خروجی: [3,3]

توضیح: دو نکته مهم وجود دارد:

محدودیت ها:

تعداد گره ها در لیست در محدوده است [2, 105].
1 5

راه حل:

/**
* Definition for a singly-linked list.
* class ListNode {
* public $val = 0;
* public $next = null;
* function __construct($val = 0, $next = null) {
* $this->val = $val;
* $this->next = $next;
* }
* }
*/
class Solution {

/**
* @param ListNode $head
* @return Integer[] */
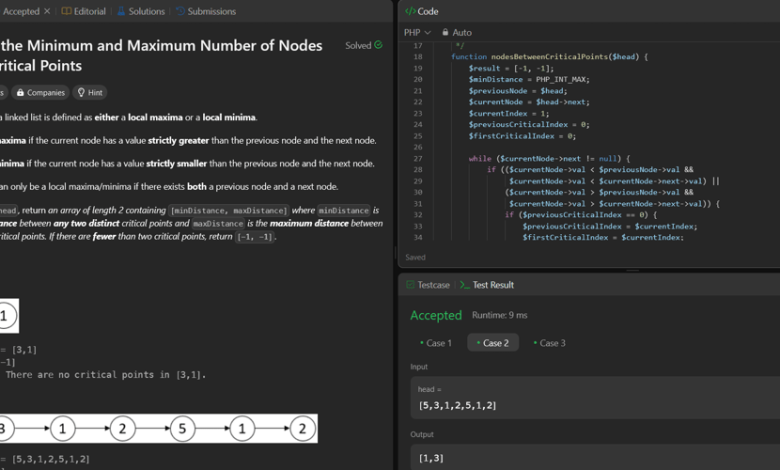
function nodesBetweenCriticalPoints($head) {
$result = [-1, -1];

// Initialize minimum distance to the maximum possible value
$minDistance = PHP_INT_MAX;

// Pointers to track the previous node, current node, and indices
$previousNode = $head;
$currentNode = $head->next;
$currentIndex = 1;
$previousCriticalIndex = 0;
$firstCriticalIndex = 0;

while ($currentNode->next != null) {
// Check if the current node is a local maxima or minima
if (($currentNode->val val &&
$currentNode->val next->val) ||
($currentNode->val > $previousNode->val &&
$currentNode->val > $currentNode->next->val)) {
// If this is the first critical point found
if ($previousCriticalIndex == 0) {
$previousCriticalIndex = $currentIndex;
$firstCriticalIndex = $currentIndex;
} else {
// Calculate the minimum distance between critical points
$minDistance = min($minDistance, $currentIndex – $previousCriticalIndex);
$previousCriticalIndex = $currentIndex;
}
}

// Move to the next node and update indices
$currentIndex++;
$previousNode = $currentNode;
$currentNode = $currentNode->next;
}

// If at least two critical points were found
if ($minDistance != PHP_INT_MAX) {
$maxDistance = $previousCriticalIndex – $firstCriticalIndex;
$result = [$minDistance, $maxDistance];
}

return $result;
}
}

وارد حالت تمام صفحه شوید

از حالت تمام صفحه خارج شوید

/**
 * Definition for a singly-linked list.
 * class ListNode {
 *     public $val = 0;
 *     public $next = null;
 *     function __construct($val = 0, $next = null) {
 *         $this->val = $val;
 *         $this->next = $next;
 *     }
 * }
 */
class Solution {

    /**
     * @param ListNode $head
     * @return Integer[]
     */
    function nodesBetweenCriticalPoints($head) {
        $result = [-1, -1];

        // Initialize minimum distance to the maximum possible value
        $minDistance = PHP_INT_MAX;

        // Pointers to track the previous node, current node, and indices
        $previousNode = $head;
        $currentNode = $head->next;
        $currentIndex = 1;
        $previousCriticalIndex = 0;
        $firstCriticalIndex = 0;

        while ($currentNode->next != null) {
            // Check if the current node is a local maxima or minima
            if (($currentNode->val val &&
                    $currentNode->val next->val) ||
                ($currentNode->val > $previousNode->val &&
                    $currentNode->val > $currentNode->next->val)) {
                // If this is the first critical point found
                if ($previousCriticalIndex == 0) {
                    $previousCriticalIndex = $currentIndex;
                    $firstCriticalIndex = $currentIndex;
                } else {
                    // Calculate the minimum distance between critical points
                    $minDistance = min($minDistance, $currentIndex - $previousCriticalIndex);
                    $previousCriticalIndex = $currentIndex;
                }
            }

            // Move to the next node and update indices
            $currentIndex++;
            $previousNode = $currentNode;
            $currentNode = $currentNode->next;
        }

        // If at least two critical points were found
        if ($minDistance != PHP_INT_MAX) {
            $maxDistance = $previousCriticalIndex - $firstCriticalIndex;
            $result = [$minDistance, $maxDistance];
        }

        return $result;
    }
}