چگونه من شهود را در پشت مدل Arima به دست آوردم

خلاصه

در این مقاله ، ما تکنیک های پیش بینی را با تمرکز بر Arima ، یک مدل پیش بینی سری زمانی قدرتمند بررسی می کنیم. قبل از غواصی به آریما ، ابتدا با پوشش دادن یک پایه محکم می سازیم:

1. انواع پیش بینی – کیفی در مقابل کمی
2. شرط کلیدی برای پیش بینی-اهمیت ثابت بودن و نحوه بررسی آن با استفاده از آزمون افزودنی Dickey-Fuller (ADF)
3. روشهای پیش بینی کمی – ساده لوح ، حرکت متوسط ​​و صاف کردن نمایی
4. تجزیه Arima – درک اجزای آن قدم به قدم:
   • مدل اتورگرایی (AR) – چگونه مقادیر گذشته بر پیش بینی ها تأثیر می گذارد ، با استفاده از عملکرد همبستگی جزئی (PACF) مشخص می شود
   • مدل متوسط ​​(MA) مدل – چگونه خطاهای گذشته بر پیش بینی ها تأثیر می گذارد ، با استفاده از عملکرد همبستگی (ACF) مشخص می شود
   • مدل ARMA – ترکیب AR و MA برای پیش بینی بهتر
   • مدل ARIMA – اضافه کردن تفاوت برای رسیدگی به روند و دستیابی به ثابت بودن
5. اجرای گام به گام-یک نمونه کدگذاری عملی با استفاده از پایتون

در پایان ، شما یک رویکرد ساختاری برای درک و اجرای ARIMA برای پیش بینی سری زمانی خواهید داشت. بیایید شیرجه بزنیم!

چرا آریما؟

من فکر کردم که من هنوز چه مفاهیمی را در داده ها کشف نمی کنم. چیزهای زیادی بود!

اما من متوجه بسیاری از تجزیه و تحلیل داده ها شدم که تقاضای شغل را پیش بینی کرد و فکر کردم چرا نه. من شهود پشت آن را فهمیدم و آرزو می کردم راهی ساده تر برای قرار دادن همه آن وجود داشته باشد.

علاوه بر این ، پیش بینی یادگیری به نظر می رسد که در انواع برنامه های کاربردی استفاده می شود.

از آریما استفاده می شود؟

• بازار سهام: قیمت سهام و روند بازار را پیش بینی می کند.
• پیش بینی تقاضا: به مشاغل کمک می کند تا تقاضای محصول آینده برای مدیریت موجودی را پیش بینی کنند.
• پیش بینی فروش: پیش بینی درآمد و روند فروش برای کمک به برنامه ریزی استراتژیک.
• اقتصاد: برای پیش بینی نرخ تورم و سایر شاخص های اقتصادی استفاده می شود.
• پیش بینی آب و هوا: به پیش بینی دما ، بارندگی و سایر الگوهای آب و هوا کمک می کند.
• بهداشت و درمان: شیوع بیماری و خواسته های منابع بهداشتی را پیش بینی می کند.

من به سرعت مباحثی را که خوانده ام قبل از شروع ARIMA لیست می کنم تا اصول اولیه را بدست آورید.

قسمت 1: انواع تکنیک های پیش بینی

ما قصد داریم در تکنیک های کمی تمرکز کنیم.

قسمت 2: شرط مشترک برای یادآوری

شرط: بسیاری از مدل های پیش بینی نیاز به داده ها دارند (خاصیت آماری مانند میانگین ، واریانس باید ثابت بماند). اگر داده های غیر ثابت ما متفاوت انجام می دهیم (داده های فعلی را از گذشته تفریق می کنیم).

بنابراین چگونه می توانیم بدانیم که یک داده ثابت است یا خیر؟

ما از تست دیکی فولر استفاده می کنیم

قسمت 3: تکنیک های پیش بینی کمی

• روش ساده لوح (ارزش امروز دقیقاً مثل دیروز خواهد بود)
• روش متوسط ​​حرکت (ارزش امروز به طور متوسط ​​روزهای گذشته خواهد بود)
• هموار سازی نمایی (ارزش امروز بیشتر از روزهای قبل تحت تأثیر روز اخیر خواهد بود)

قسمت 4: آریما.

نفرین یادگیری توسط خودتان این است که خواهید فهمید که چگونه باید قبلاً آن را تکمیل کرده اید.

به همین ترتیب ، هنگامی که من مستقیماً به یادگیری مدل Arima پریدم ، با مفاهیمی مانند ترتیب P ، D ، Q ، Lags ، Arima (P ، D ، Q) و غیره بمباران شدم ، و همه آنها هیچ سرنخی در مورد آن نداشتم.

وقتی فهمیدم که چگونه باید این مفهوم را آموختم ، فکر کردم چرا به دیگران اجازه نمی دهم که چه چیزی برای من کار کرده است زیرا ممکن است برای دیگران نیز کار کند. من فهمیدم که مؤلفه های ARIMA مدلهای پیش بینی ریاضی فردی هستند که ابتدا باید به طور جداگانه درک شوند.

اینجا می رود …

مرحله 1: درک مدل AR (خودکار رگرسیون)

مدل AR چیست؟

مدل Autoregressive (AR) یک سری زمانی را به عنوان یک تابع خطی از مقادیر گذشته خود بیان می کند. تعداد مقادیر گذشته مورد استفاده به عنوان P (دستور خودکار) مشخص شده است.

معادله مدل AR:

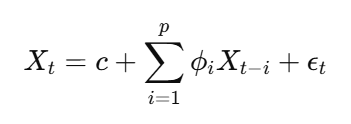
کجا

بنابراین ما معادله داریم ، اما P چیست؟

بله ، ما می دانیم که این تعداد ارزش های گذشته است.

اما چگونه می توانیم تعداد بهینه مقادیر گذشته را پیدا کنیم که باید در فرمول گنجانده شود؟

برای همین ما ، چیزی به نام PACF (عملکرد همبستگی جزئی) که به ما کمک می کند تا تعداد مقادیر گذشته را که در مدل AR گنجانده شده است ، تعیین کنیم. Note: Only Basic intuition behind PACF and ACF is explained in this article

PACF چگونه P را نشان می دهد؟

PACF جلوه های غیرمستقیم را از بین می برد و تنها همبستگی مستقیم بین یک سری زمانی و مقادیر گذشته آن را نشان می دهد.

به زبان ساده
مقدار روز 5 می تواند مستقیماً تحت تأثیر روز 4 باشد که نمونه ای از اثر مستقیم است
مقدار روز 5 می تواند تحت تأثیر روز 4 باشد که خود تحت تأثیر روز 3 نمونه ای از اثر غیرمستقیم است.
بنابراین ، با استفاده از PACF می توانیم تأثیرات مستقیم روز 1 ، روز 2 ، روز 3 و روز 4 را در روز 5 ارزش مشاهده کنیم.

با این حال ، چگونه می توانیم P را از PACF بفهمیم؟

مقدار P اولین تاخیر قابل توجهی است که در آن طرح PACF قطع می شود.

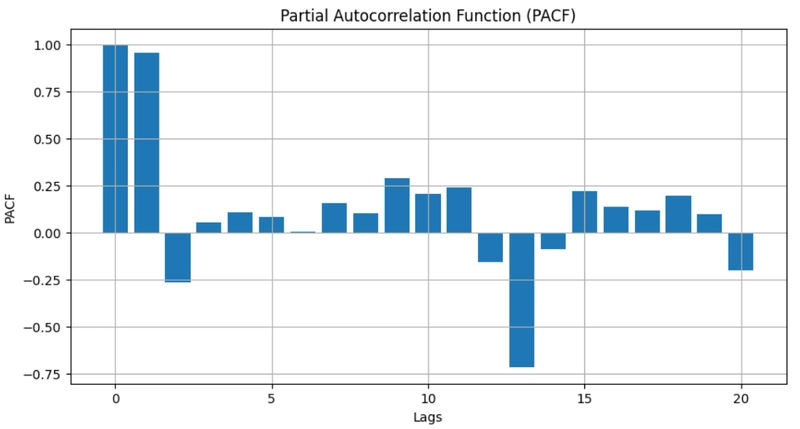
اعتبار تصویر: geeksforgeeks

در اینجا P مقدار تاخیر است که مقدار PACF مثبت را داده و درست بعد از آن به صفر می رسد. بنابراین این تاخیر 2 است بنابراین مؤلفه AR (2) راه حل مناسب است.

مرحله 2: درک مدل MA (میانگین متحرک)

این دقیقاً مانند مدل AR است اما به جای مقادیر گذشته ، این مدل از خطاهای گذشته استفاده می کند.

مدل MA چیست؟

مدل میانگین متحرک (MA) سری زمانی را به عنوان یک تابع خطی از اصطلاحات خطای گذشته بیان می کند. تعداد خطاهای گذشته مورد استفاده به عنوان Q (سفارش متوسط ​​در حال حرکت) مشخص شده است.

معادله مدل MA:

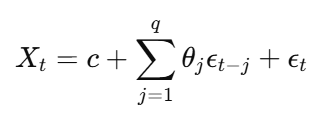
کجا:

بنابراین چگونه Q را پیدا می کنیم؟

• درست مانند گذشته ، در اینجا ما از ACF (عملکرد همبستگی) استفاده می کنیم تا به ما کمک کند تا تعداد اصطلاحات خطای گذشته را در مدل MA درج کنیم.
• ACF همبستگی ها را در تاخیر مختلف ، از جمله اثرات مستقیم و غیرمستقیم اندازه گیری می کند.
• مقدار Q اولین تاخیر قابل توجهی است که در آن قطعه ACF قطع می شود.

مرحله 3: ترکیب مدل های AR و MA – ARMA

اکنون هر دوی آنها را ترکیب می کنیم تا یک مدل ARMA شکل بگیریم. مدل ARMA (P ، Q) ترکیبی از مدل های AR و MA است که هم مقادیر گذشته و هم خطاهای گذشته را به خود اختصاص می دهد.

معادله مدل ARMA: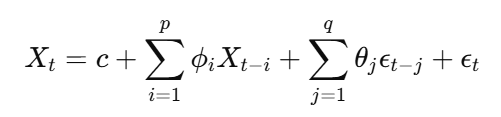

مراحل شناسایی یک مدل ARMA:

1. برای تعیین (سفارش AR) از PACF استفاده کنید.
2. برای تعیین (سفارش MA) از ACF استفاده کنید.
3. با استفاده از این مقادیر ، مدل ARMA را متناسب کنید.

مرحله 4: معرفی تفاوت – ARIMA

چرا تفاوت لازم است؟

شرایط مشترک ما را به خاطر بسپار ، به همین دلیل است. اگر یک سری زمانی یک روند (رفتار غیر ثابت) داشته باشد ، مدل های AR و MA به تنهایی به طور مؤثر کار نمی کنند. برای اینکه این سریال ثابت شود ، ما متفاوت است.

بنابراین ، تفاوت چیست؟

متفاوت با کم کردن هر مقدار از مقدار قبلی ، روند را از بین می برد

سرانجام ، قهرمان داستان

معادله مدل ARIMA:

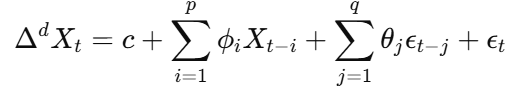
این شبیه به معادله قبلی است اما فقط Delta D گنجانده شده است.
کجا

مراحل شناسایی یک مدل ARIMA:

1. با استفاده از آزمون افزودنی Dickey-Fuller (ADF) ، ثابت بودن را بررسی کنید.
2. اگر غیر ثابت است ، تا زمانی که این سری ثابت باشد ، تفاوت را اعمال کنید (D پیدا کنید).
3. برای تعیین P (AR) از PACF استفاده کنید.
4. برای تعیین Q (سفارش MA) از ACF استفاده کنید.
5. با استفاده از مقادیر مشخص شده ، مدل ARIMA را متناسب کنید.

کد مثال توسط chatgpt برای مرجع

Step 1: Import Libraries

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
Step 2: Load and Visualize Data

# Sample monthly sales data (dummy example)
data = {
    "Month": pd.date_range(start="2018-01-01", periods=60, freq="M"),
    "Sales": [150, 160, 165, 170, 180, 190, 200, 210, 215, 220, 230, 240,
              250, 260, 270, 280, 290, 300, 310, 320, 325, 330, 340, 350,
              360, 370, 380, 390, 400, 410, 420, 430, 440, 450, 460, 470,
              480, 490, 500, 510, 520, 530, 540, 550, 560, 570, 580, 590,
              600, 610, 620, 630, 640, 650, 660, 670, 680, 690, 700, 710]
}

df = pd.DataFrame(data)
df.set_index("Month", inplace=True)

# Plot the time series
plt.figure(figsize=(10, 5))
plt.plot(df, marker="o", linestyle="-", label="Sales Data")
plt.xlabel("Year")
plt.ylabel("Sales")
plt.title("Monthly Sales Data")
plt.legend()
plt.show()
Observation: The data shows an increasing trend, so we may need differencing.

Step 3: Check for Stationarity
Before applying ARIMA, we check if the time series is stationary 
using the Augmented Dickey-Fuller (ADF) test.

# ADF Test
result = adfuller(df["Sales"])
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')

# If p-value > 0.05, the data is non-stationary
If the p-value > 0.05, the series is not stationary, 
meaning we need to apply differencing.

Step 4: Apply Differencing (If Needed)

df_diff = df.diff().dropna()

# Plot differenced data
plt.figure(figsize=(10, 5))
plt.plot(df_diff, marker="o", linestyle="-", label="Differenced Sales Data")
plt.xlabel("Year")
plt.ylabel("Sales Difference")
plt.title("Differenced Monthly Sales Data")
plt.legend()
plt.show()

# ADF test on differenced data
result = adfuller(df_diff["Sales"])
print(f'ADF Statistic after Differencing: {result[0]}')
print(f'p-value: {result[1]}')
If the p-value < 0.05, the series is now stationary, 
and we can proceed with ARIMA.

Step 5: Identify ARIMA Parameters (p, d, q)
We use Autocorrelation Function (ACF) and Partial 
Autocorrelation Function (PACF) plots to 
determine the values of 𝑝 (AR term) and 𝑞 (MA term).

# ACF and PACF plots
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
plot_acf(df_diff, ax=ax[0])
plot_pacf(df_diff, ax=ax[1])
plt.show()
From ACF: The point where it sharply cuts off suggests 
𝑞
q (MA order).

From PACF: The point where it sharply cuts off suggests 
𝑝
p (AR order).

Based on the plots, let's assume ARIMA(1,1,1).

Step 6: Fit ARIMA Model

# Fit ARIMA(1,1,1)
model = sm.tsa.ARIMA(df["Sales"], order=(1,1,1))
model_fit = model.fit()

# Print model summary
print(model_fit.summary())
Step 7: Forecast Future Values
We forecast the next 12 months.


# Forecast next 12 months
forecast = model_fit.forecast(steps=12)

# Create forecast dates
future_dates = pd.date_range(start=df.index[-1], periods=13, freq="M")[1:]
forecast_df = pd.DataFrame({"Month": future_dates, "Forecast": forecast})
forecast_df.set_index("Month", inplace=True)

# Plot actual data vs forecast
plt.figure(figsize=(10, 5))
plt.plot(df, marker="o", label="Actual Sales")
plt.plot(forecast_df, marker="o", linestyle="dashed", label="Forecast")
plt.xlabel("Year")
plt.ylabel("Sales")
plt.title("Sales Forecast using ARIMA(1,1,1)")
plt.legend()
plt.show()