درک پیچیدگی الگوریتم: شیرجه عمیق به نماد O بزرگ با جاوا اسکریپت

Summarize this content to 400 words in Persian Lang
سلام !! مدتی است که به دلیل اتفاقات، سخنرانی ها، کارها و … مقالاتی منتشر نمی کنم.

ولی کم کم برمیگردم! اما بعد، همانطور که همیشه می پرسم، چطوری؟ همه خوبن؟ همه چیز در آرامش؟ امیدوارم حالتون خوب باشه!

امروز می‌خواهم محتوای فوق‌العاده متفاوتی را به شما ارائه کنم، در ابتدا ممکن است کمی پیچیده باشد، اما در بسیاری از مصاحبه‌ها (برای فناوری‌های بزرگ) این سؤالات اغلب پرسیده می‌شود. تحلیل پیچیدگی الگوریتم!

این یک مفهوم بسیار مهم است! اگر هرگز تحلیل پیچیده الگوریتم یا O big را در یک محیط دانشگاهی پوشش نداده اید، مطمئن باشید! من سعی می کنم به روشی ساده به آن بپردازم که شما بتوانید درک کنید! اما من قصد ندارم خیلی عمیق به موضوع بپردازم، زیرا انجام آن یک سال دانشگاهی کامل طول می کشد.

بیگ O

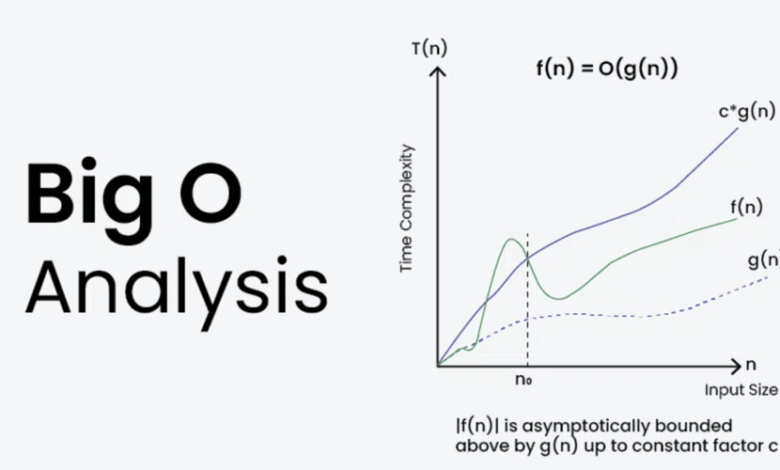
Big O زبان و متریکی است که برای توصیف کارایی الگوریتم ها استفاده می کنیم. گاهی اوقات لازم است توضیح دهیم که آیا الگوریتم ما کارآمد است یا خیر، و این تجزیه و تحلیل زمانی مهم است که به دنبال عملکرد باشیم یا ارزیابی کنیم که آیا الگوریتم ما کارآمد است.

سناریوی زیر را تصور کنید: شما یک فایل روی یک هارد دیسک دارید و باید آن را برای دوست خود که در سراسر کشور زندگی می کند ارسال کنید. شما باید فایل را در اسرع وقت به دوست خود برسانید. چگونه باید آن را ارسال کنید؟

برخی از مردم پیشنهاد می کنند، FTP؟ ایمیل؟ گوگل درایو؟ اگر فایل کوچکی است، مطمئناً حق با شماست. احتمالاً 5 تا 10 ساعت طول می کشد تا به فرودگاه برسید، هواپیما را بگیرید و آن را به دوست خود تحویل دهید.

اگر فایل واقعاً بزرگ بود چه می شد. مثلا 1 ترابایت؟ انتقال الکترونیکی فایل ممکن است بیش از یک روز طول بکشد. احتمالاً پرواز در سراسر کشور بسیار سریعتر خواهد بود.

این مفهوم زمان اجرا مجانبی یا زمان بزرگ O است.

O(1) نمونه ای از تحویل با استفاده از هواپیما خواهد بود. O(1) با توجه به اندازه فایل. زمان ثابت است.

O(n) نمونه ای با استفاده از انتقال الکترونیکی است. که در آن N، اندازه فایل است. این بدان معنی است که زمان انتقال فایل به صورت خطی با اندازه فایل افزایش می یابد.

خط سبز O(n) و خط آبی O(1) است.

زمان های اجرا بسیار بیشتر از این وجود دارد. برخی از رایج ترین آنها عبارتند از O(log n)، O(n * log n)، O(n)، O(nˆ2)، O(2ˆn).

بهترین حالت، بدترین حالت و مورد انتظار

ما در واقع می توانیم زمان اجرا خود را برای یک الگوریتم به سه روش مختلف توصیف کنیم:

الگوریتم مرتب سازی سریع را تصور کنید:

function quickSort(arr) {

if (arr.length <= 1) {
return arr;
}

const pivot = arr[arr.length – 1];
const left = [];
const right = [];

for (let i = 0; i < arr.length – 1; i++) {
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}

return […quickSort(left), pivot, …quickSort(right)];
}

وارد حالت تمام صفحه شوید

از حالت تمام صفحه خارج شوید

در حال حاضر، از بازگشت مجدد نترسید. مرتب‌سازی سریع یک عنصر تصادفی را به‌عنوان «پیوت» انتخاب می‌کند و سپس مقادیری را در آرایه مبادله می‌کند تا عنصر کمتر از محور قبل از عناصر بزرگ‌تر از محور ظاهر شود. این یک “مرتب سازی جزئی” می دهد. سپس به صورت بازگشتی سمت چپ و راست را با استفاده از یک فرآیند مشابه مرتب می کند.

بهترین مورد: اگر همه عناصر برابر باشند، مرتب سازی سریع به طور متوسط ​​فقط یک بار از طریق آرایه عبور می کند. این O(n) است.
بدترین حالت: اگر واقعاً بدشانسی بیفتیم و پیوت مکرراً بزرگترین عنصر آرایه باشد چه؟ در این حالت، بازگشت ما آرایه را به نصف تقسیم نمی‌کند و هر نیمه را تکرار نمی‌کند. فقط زیرآرایه را با یک عنصر کوچک می کند. این به زمان اجرا O(nˆ2) تبدیل می شود.

پیچیدگی فضا

زمان تنها چیزی نیست که در یک الگوریتم مهم است. همچنین ممکن است به مقدار حافظه یا فضا اهمیت دهیم. تصور کنید با دستگاه های کم حافظه مانند اینترنت اشیا کار می کنیم.

پیچیدگی فضا مفهومی موازی با پیچیدگی زمانی است. اگر ما نیاز به ایجاد یک آرایه به اندازه N داشته باشیم. این به فضای O(n) نیاز دارد. اگر به یک آرایه دو بعدی (ماتریسی) از nxn نیاز داشته باشیم، این به فضای O(n^2) نیاز دارد.

احتمالاً قبلاً این خطاها را دیده اید:

سرریز پشته
سرریز حافظه

همچنین در تعداد تماس‌های مجدد، فضای پشته را جمع کنید:

function sum(n) {
if (n <= 0)
return 0;

return n + sum(n-1);
}

وارد حالت تمام صفحه شوید

از حالت تمام صفحه خارج شوید

برای مثال، کدی مانند این زمان O(n) و فضای O(n) را می گیرد.

زمان های بازگشتی

احتمالاً قبلاً در مورد فیبوناچی در ریاضیات شنیده اید.دنباله فیبوناچی مجموعه ای از اعداد است که هر عدد مجموع دو عدد قبلی است. معمولاً با 0 و 1 شروع می شود. دنباله به صورت زیر است:

0، 1، 1، 2، 3، 5، 8، 13، 21، 34، …

حالا الگوریتم:

function fibonacci(n) {
if (n <= 1)
return 1;

return fibonacci(n-1) + fibonacci(n-1);
}

وارد حالت تمام صفحه شوید

از حالت تمام صفحه خارج شوید

بسیاری از مردم بنا به دلایلی این دو تماس را مشاهده خواهند کرد fibonacci و به O(nˆ2) بپرید. این کاملا اشتباه است.

پیچیدگی فضایی این الگوریتم O(n) خواهد بود. اگرچه در کل درخت گره های O(2^n) داریم، در هر زمان معین فقط O(n) وجود دارد.

حالا زمان اجرای کد زیر چقدر است؟

function foo(array) {
let sum = 0;
let product = 1;

array.forEach(item => {
sum += item;
});

array.forEach(item => {
product *= item;
});

console.log(`${sum}, ${product}`);
}

وارد حالت تمام صفحه شوید

از حالت تمام صفحه خارج شوید

اگر به O(n) پاسخ دهید. بله حق با شماست! این واقعیت که ما از طریق آرایه دو بار تکرار می کنیم، مهم نیست.

حالا یک مثال دیگر:

function printPairs(array) {
for(let i = 0; i < array.length; i++) {
for(let j = 0; j< array.length; j++) {
console.log(`${array[i]} , ${array[j]}`);
}
}
}

وارد حالت تمام صفحه شوید

از حالت تمام صفحه خارج شوید

زمان اجرا O(n^2) است.

بنابراین اکنون می توانید این مفاهیم تحلیل پیچیدگی زمان و مکان الگوریتم ها را درک کنید! البته بسیاری از مفاهیم دیگر مانند تتای بزرگ، امگا بزرگ، زمان استهلاک، درختان و بازگشت پیچیده‌تر را که در اینجا به آنها اشاره نکردم.

اما این یک مفهوم سخت است! و اکنون وقتی در مورد پیچیدگی زمانی یا مکانی یک الگوریتم سوال می شود متوجه می شوید.

این همه مردمی! امیدوارم خوشتون اومده باشهاگر من به شما کمک کردم، این پست را لایک کنید، من را در شبکه های اجتماعی من دنبال کنید!

لینکدین: https://www.linkedin.com/in/kevin-uehara/اینستاگرام: https://www.instagram.com/uehara_kevin/توییتر: https://x.com/ueharaDevGithub: https://github.com/kevinueharadev.to: https://dev.to/kevin-ueharaیوتیوب: https://www.youtube.com/@ueharakevin/

function quickSort(arr) {

    if (arr.length <= 1) {
        return arr;
    }


    const pivot = arr[arr.length - 1];
    const left = [];
    const right = [];

    for (let i = 0; i < arr.length - 1; i++) {
        if (arr[i] < pivot) {
            left.push(arr[i]);
        } else {
            right.push(arr[i]);
        }
    }

    return [...quickSort(left), pivot, ...quickSort(right)];
}

function sum(n) {
 if (n <= 0)
  return 0;

 return n + sum(n-1);
}

function fibonacci(n) {
 if (n <= 1)
  return 1;

 return fibonacci(n-1) + fibonacci(n-1);
}

function foo(array) {
 let sum = 0;
 let product = 1;

 array.forEach(item => {
  sum += item;
 });

 array.forEach(item => {
  product *= item;
 });

 console.log(`${sum}, ${product}`);
}

function printPairs(array) {
  for(let i = 0; i < array.length; i++) {
   for(let j = 0; j< array.length; j++) {
    console.log(`${array[i]} , ${array[j]}`);
   }
  }
}