مقدمه ای بر محاسبات کوانتومی

محاسبات کوانتومی اینجا، محاسبات کوانتومی آنجا، محاسبات کوانتومی در همه جا! آیا می‌توانیم از آن منطقی بسازیم؟ من دوست دارم وقتی مردم در مورد آن صحبت می کنند کاملاً احساس نابجایی نداشته باشم، پس بیایید با هم آن را بفهمیم!

من این سری از پست ها را درباره محاسبات کوانتومی شروع کردم برای یادگیری شخصیبه منظور درک مفاهیم کلی آن در جامعه مدرن ما و اینکه چگونه می تواند بر زندگی روزمره من با فناوری تأثیر بگذارد.. من ادعا نمی کنم که در این موضوع متخصص هستم و این بیشتر یادداشت های من بر اساس چیزهایی است که با خواندن مقالات یاد می گیرم و از ChatGPT می خواهم آنچه را که می خوانم ساده کند 😀

محاسبات کوانتومی یک فناوری جدید انقلابی است که از اصول استفاده می کند مکانیک کوانتومی (شاخه پیچیده ای از فیزیک که شگفتی های قلمرو زیراتمی را بررسی می کند و سعی می کند ماهیت ذرات را توضیح دهد تا اصول اساسی حاکم بر جهان ما را کشف کند — اما امروز برای این کار اینجا نیستیم) تا اطلاعات را با سرعتی باورنکردنی پردازش کند.

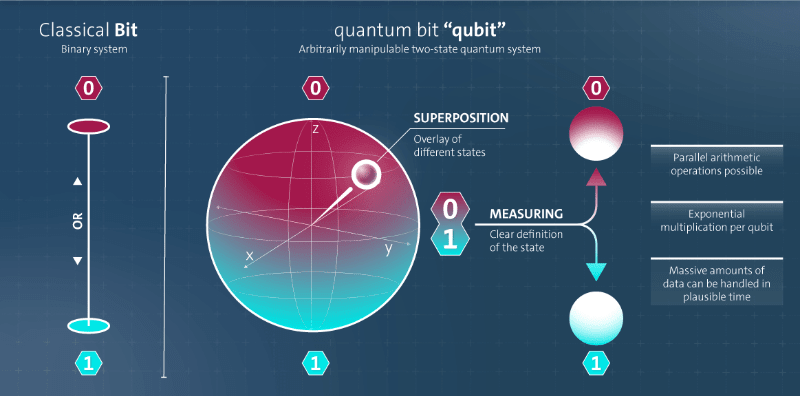
برخلاف رایانه‌های کلاسیک که اطلاعات را با استفاده از بیت‌های 0 یا 1 ذخیره و پردازش می‌کنند، رایانه‌های کوانتومی از بیت‌های کوانتومی یا کیوبیت ها، که می تواند در چندین حالت به طور همزمان وجود داشته باشد، به این معنی که یک کیوبیت می تواند هم 0 و هم 1 باشد. … اما چگونه؟

برهم نهی

بیایید در مورد ایده صحبت کنیم برهم نهی، که شرح می دهد توانایی یک کیوبیت برای وجود همزمان در چندین حالت. اگر یک بیت معمولی می تواند به عنوان یک حالت نیز باشد 0 یا 1، وضعیت کیوبیت را می توان به صورت نمایش داد

|ψ⟩ = α|0⟩ + β|1⟩

که نیاز به توضیح کامل دارد، اما به طور خلاصه:

1. علامت |ψ⟩ وضعیت کیوبیت را نشان می دهد. ψ فقط یک نام متغیر است و |⟩ نمادها مانند براکت هایی هستند که نشان می دهند حالت کوانتومی است.
2. را α|0⟩ و β|1⟩ شرایط هستند دامنه های احتمال. آنها نشان دهنده شانس یافتن کیوبیت در ایالت ها هستند |0⟩ و |1⟩
3. α دامنه احتمال یافتن کیوبیت را نشان می دهد |0⟩ حالت؛
4. β دامنه احتمال یافتن کیوبیت را نشان می دهد |1⟩ حالت.

(… و بله، چون مجبور شدم از خودم بپرسم، دامنه های احتمال اعداد کاملاً پیچیده ای هستند، اما اصل آنها این است که مجموع α و β به 1 می رسد، به این معنی که مجموع احتمالات همه نتایج ممکن است. همیشه برابر با 1 است.)

می‌توانیم وضعیت یک کیوبیت را مانند یک نقطه روی یک توپ به نام the تصور کنیم کره بلوخ. اعداد α و β تعیین می کنند که نقطه کیوبیت دقیقاً کجا روی توپ باشد. اگر α و β اعداد منظمی باشند، نقطه کیوبیت مانند خط استوا در وسط سطح توپ قرار دارد. این بدان معنی است که کیوبیت به همان اندازه ترکیبی از |0⟩ و |1⟩. اما اگر α و β اعداد مختلط باشند (در مورد اعداد مختلط در Math Is Fun بیشتر بخوانید)، نقطه کیوبیت در جای دیگری روی سطح توپ است. این بدان معنی است که کیوبیت ترکیبی کلی تر از آن است |0⟩ و |1⟩.

وقتی یک کیوبیت در برهم نهی قرار دارد، مثل این است که در حال کاوش همه حالات ممکن به یکباره است. با این حال، وقتی کیوبیت را اندازه می گیریم، آن را فرو می ریزد به حالت معین، یا 0 یا 1. عمل اندازه‌گیری کیوبیت را مجبور می‌کند یکی از احتمالات را انتخاب کند و از آن نقطه به بعد، مانند یک بیت کلاسیک رفتار می‌کند..

به عنوان مثال، اگر |α|^2 = 0.4 و |β|^2 = 0.6، اندازه گیری احتمال بیشتری دارد که نتیجه 1 را به دست آورد، اما هنوز شانس به دست آوردن نتیجه 0 وجود دارد.

خوب، اما… چگونه یک کیوبیت را در برهم نهی تنظیم می کنید؟

برای انجام این کار، می توانیم از یک خاص استفاده کنیم دروازه کوانتومی معروف به دروازه هادامارد (دروازه H) (در مورد دروازه کوانتومی بعداً :D). دروازه هادامارد برهم نهی برابری از |0⟩ و |1⟩ حالت برای یک کیوبیت. در اینجا توضیح ساده ای از نحوه عملکرد آن آورده شده است:

1. با یک کیوبیت شروع کنید |0⟩ ایالت یا |1⟩ حالت
2. استفاده از دروازه هادامارد (H دروازه) به کیوبیت
3. اگر کیوبیت در ابتدا در |0⟩ حالت، دروازه H آن را در برهم نهی برابر قرار می دهد |0⟩ و |1⟩. حالت حاصل خواهد بود (|0⟩ + |1⟩) / √2، یعنی کیوبیت در هر دو حالت به طور همزمان است
4. اما، اگر کیوبیت در ابتدا در |1⟩ حالت، دروازه H دوباره آن را در یک برهم نهی برابر قرار می دهد |0⟩ و |1⟩ اما حالت حاصل خواهد بود (|0⟩ - |1⟩) / √2، به این معنی که کیوبیت در هر دو حالت است اما با تغییر فاز (که موضوع بسیار پیچیده تری است و من هنوز به دنبال یافتن مطالب خوب و ساده در مورد آن هستم — در قسمت نظرات زیر به اشتراک بگذارید!).

خواندن مقادیر چند کیوبیت به طور مشابه کار می کند، با هر کیوبیت به طور جداگانه اندازه گیری می شود، و نتایج ترکیب می شوند تا یک رشته بیت کلاسیک یا یک حالت کوانتومی در مورد درهم تنیدگی. که ما را به نقطه بعدی هدایت می کند…

در هم تنیدگی

مفهوم مهم دیگر در محاسبات کوانتومی این است در هم تنیدگی، که پدیده ای را توصیف می کند اتصال دو یا چند کیوبیت به گونه ای که به آنها اجازه می دهد بر رفتار یکدیگر تأثیر بگذارند، حتی اگر با فواصل زیاد از هم جدا شوند. اساساً درهم تنیدگی همبستگی های آنی بین نتایج اندازه گیری آنها ایجاد می کند که در سه مرحله انجام می شود:

• آماده سازی: دو یا چند کیوبیت در کنار هم قرار می گیرند و به روشی خاص با یکدیگر تعامل دارند از طریق یک عملیات دروازه کوانتومی (موضوع بسیار طولانی است که در حال حاضر نمی توان در اینجا به آن پرداخت، اما Universal Quantum یک مقاله عالی در مورد Medium در مورد دروازه های کوانتومی دارد).
• دولت حاصل: در نتیجه این برهمکنش کیوبیت ها در هم پیچیده می شوند و a به اشتراک می گذارند حالت کوانتومی مشترک، که نمی تواند به عنوان یک ترکیب ساده از حالت های کیوبیت منفرد بیان شود حالت درهم تنیده کل سیستم را به عنوان یک کل در بر می گیرد نه اینکه هر کیوبیت را به طور مستقل توصیف کند..
• همبستگی ها: نتایج اندازه گیری یک کیوبیت به طور آنی با نتایج اندازه گیری دیگری (های) همبستگی دارد. این همبستگی ها صرف نظر از جدایی فیزیکی بین کیوبیت های درهم تنیده درست است، که اغلب از آن به عنوان غیر محلی یا اقدام شبح آور از راه دور (یک بار دیگر، یک موضوع برای بار دیگر).

مختصری در مورد دروازه های کوانتومی

اینجاست که بعد از دروازه هادامارد که قبلاً به آن اشاره کردیم شروع به از دست دادن آن می کنم. جای خوبی به نظر می رسد که در آن باید بیشتر به خواندن ادامه دهم تا زمانی که به اندازه کافی اعتماد به نفس برای نوشتن یادداشت در مورد موضوع داشته باشم 😎 به هر حال…

دروازه کوانتومی یک دستورالعمل (یا عملیات) است که می توانیم از آن برای تغییر وضعیت کیوبیت ها استفاده کنیم. درست مانند اینکه چگونه عملیات ریاضی مانند جمع یا ضرب اعداد را تبدیل می کند، دروازه کوانتومی حالت کوانتومی کیوبیت ها را تغییر می دهد، هر دروازه تأثیر خاصی روی کیوبیت ها دارد: چرخش حالت، چرخاندن آن، یا قرار دادن آن در یک برهم نهی و هر چیز دیگری.

اساساً، آنها بلوک های سازنده ای هستند که به ما کمک می کنند تا قدرت محاسبات کوانتومی را دستکاری و استفاده کنیم. بار دیگر، Universal Quantum یک مقاله عالی در مورد Medium در مورد دروازه‌های کوانتومی دارد و من توصیه می‌کنم چیز دیگری را خودتان بررسی کنید (و اگر احساس سخاوت دارید، از به اشتراک گذاشتن چند لینک خوب با من نترسید:D)

مختصری در مورد چالش ها

به نظر منصفانه به نظر می رسد، قبل از بسته شدن، ذکر شود که چرا این فناوری هنوز فراگیر نشده است و چه چیزهایی باید بر آنها غلبه کند.

یکی از چالش های اصلی در ساخت یک کامپیوتر کوانتومی، ماهیت ظریف کیوبیت ها است. از آنجا که آنها بر اساس اصول مکانیک کوانتومی هستند، کیوبیت ها به راحتی تحت تاثیر محیط خود قرار می گیرندو می تواند به راحتی توسط عوامل خارجی مانند دما، نویز یا حتی نور مختل شود. این امر کنترل و دستکاری کیوبیت ها و حفظ حالت کوانتومی آنها را برای مدت طولانی دشوار می کند.

با وجود این چالش ها، محققان در سال های اخیر پیشرفت قابل توجهی در توسعه کامپیوترهای کوانتومی داشته اند. در سال 2019، گوگل اعلام کرد که رایانه کوانتومی آن با حل مشکلی که برای رایانه های کلاسیک غیرممکن است در مدت زمان معقول حل شود، به «برتری کوانتومی» دست یافته است. این یک نقطه عطف بزرگ در توسعه محاسبات کوانتومی بود و نشان داد که این فناوری به سرعت در حال پیشرفت است.

نتیجه گیری

خب، اینجا چه چیزی یاد گرفتیم؟

• ما یاد گرفته ایم کیوبیت ها، که بر خلاف بیت های باینری در محاسبات کلاسیک، می تواند در چندین حالت به طور همزمان وجود داشته باشد برهم نهی.
• ما همچنین کشف کردیم که یک دروازه کوانتومی خاص، دروازه هادامارد، می تواند یک کیوبیت را در این حالت برهم نهی تنظیم کند.
• علاوه بر این، کیوبیت ها می توانند باشند گرفتار، به این معنی که آنها می توانند بدون توجه به فاصله بین آنها فوراً روی یکدیگر تأثیر بگذارند.
• در نهایت، ما یک بحث کلی در مورد آن داشتیم دروازه های کوانتومی، عملیاتی که وضعیت کیوبیت ها را دستکاری می کند و به عنوان بلوک های سازنده اساسی محاسبات کوانتومی عمل می کند.

بعدش چی؟

من دوست دارم با تمرکز بیشتر به مطالعاتم ادامه دهم:

• (اول از همه، جبر خطی خود را بررسی کنم، زیرا به نظر می رسد به خواندن اسناد آنلاین کمک زیادی می کند)
• دروازه های کوانتومی
• الگوریتم های کوانتومی
• تصحیح خطای کوانتومی
• بیشتر در مورد برتری کوانتومی
• بیشتر در مورد چالش ها

ممنون که تا اینجا مطالعه کردید، اگر خواندید، و دریغ نکنید که منابع خوب را در نظرات زیر به اشتراک بگذارید اگر دوست دارید!

منابع و الهام