شکست دادن شانس: ریاضیات پشت سود کازینو

Summarize this content to 400 words in Persian Lang
آیا تا به حال فکر کرده اید که چرا کازینوها همیشه برنده می شوند؟ که در “شکست دادن شانس: ریاضیات پشت سود کازینوما ریاضیات ساده و استراتژیهای هوشمندانهای را بررسی میکنیم که تضمین میکند کازینوها در بلندمدت درآمد کسب میکنند. از طریق مثالهای قابل درک و شبیهسازیهای مونت کارلو، اسرار پشت لبه خانه را فاش خواهیم کرد. برای کشف اینکه چگونه کازینوها شانس را به نفع خود تغییر می دهند آماده شوید!
درک لبه خانه
لبه خانه یک مفهوم اساسی در دنیای کازینوها است. این نشان دهنده میانگین سودی است که کازینو انتظار دارد از هر شرط بندی بازیکنان به دست آورد. اساسا، این درصدی از هر شرط است که کازینو در دراز مدت حفظ می کند.
لبه خانه وجود دارد زیرا کازینوها شرط های برنده را بر اساس “شانس واقعی” بازی پرداخت نمی کنند. شانس واقعی نشان دهنده احتمال واقعی وقوع یک رویداد است. کازینوها با پرداخت با شانس کمی کمتر، مطمئن می شوند که در طول زمان سود می کنند.
لبه خانه (HE) به عنوان سود کازینو که به عنوان درصدی از شرط اولیه بازیکن بیان می شود، تعریف می شود.
** رولت اروپایی ** فقط یک صفر سبز دارد که در مجموع 37 عدد به آن می دهد. اگر بازیکنی 1 دلار روی قرمز شرط بندی کند، شانس 18/37 برنده شدن 1 دلار و 19/37 شانس باخت 1 دلار را دارد. مقدار مورد انتظار:
ارزش مورد انتظار=( 1 × 37/18
از این رو، در رولت اروپایی لبه خانه (HE) در اطراف است 2.7 درصد
بیایید بازی را برای خودمان بسازیم تا آن را بیشتر درک کنیم، بازی تاس انداختن ساده.
import random
def roll_dice():
roll = random.randint(1, 100)
if roll == 100:
print(roll, ‘You rolled a 100 and lost. Better luck next time!’)
return False
elif roll
وارد حالت تمام صفحه شوید
از حالت تمام صفحه خارج شوید
در این بازی:
بازیکن 1/100 شانس باخت دارد اگر رول 100 باشد.
اگر بازی بین 1 تا 50 باشد، بازیکن 50/100 شانس باخت دارد.
اگر بازی بین 51 تا 99 باشد، بازیکن 49/100 شانس برنده شدن دارد.
مقدار مورد انتظار =(1×49/100) + (-1×51/100) = 49/100 − 51/100= −2/100 ≈ −2%
بنابراین، لبه خانه است 2 درصد
آشنایی با شبیه سازی مونت کارلو
شبیهسازی مونت کارلو ابزاری قدرتمند برای درک و پیشبینی سیستمهای پیچیده با اجرای شبیهسازیهای متعدد از یک فرآیند و مشاهده نتایج است. در زمینه کازینوها، شبیهسازیهای مونت کارلو میتوانند سناریوهای مختلف شرطبندی را مدلسازی کنند تا نشان دهند که چگونه لبه خانه سودآوری بلندمدت را تضمین میکند. بیایید بررسی کنیم که شبیهسازیهای مونت کارلو چگونه کار میکنند و چگونه میتوان آنها را در یک بازی ساده کازینو اعمال کرد.
شبیه سازی مونت کارلو چیست؟
شبیه سازی مونت کارلو شامل تولید متغیرهای تصادفی برای شبیه سازی یک فرآیند چندین بار و تجزیه و تحلیل نتایج است. با انجام هزاران یا حتی میلیونها تکرار، میتوانیم توزیعی از نتایج احتمالی را به دست آوریم و بینشی در مورد احتمال وقوع رویدادهای مختلف به دست آوریم.
استفاده از شبیه سازی مونت کارلو در بازی تاس انداختن
ما از شبیه سازی مونت کارلو برای مدل سازی بازی تاس انداختن که قبلا در مورد آن صحبت کردیم استفاده خواهیم کرد. این به ما کمک می کند بفهمیم که چگونه لبه خانه بر سودآوری بازی در طول زمان تأثیر می گذارد.
`def monte_carlo_simulation(trials):
wins = 0
losses = 0
for _ in range(trials):
if roll_dice():
wins += 1
else:
losses += 1
win_percentage = (wins / trials) * 100
loss_percentage = (losses / trials) * 100
houseEdge= loss_percentage-win_percentage
print(f”After {trials} trials:”)
print(f”Win percentage: {win_percentage:.2f}%”)
print(f”Loss percentage: {loss_percentage:.2f}%”)
print(f”House Edge: {houseEdge:.2f}%”)
# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`
وارد حالت تمام صفحه شوید
از حالت تمام صفحه خارج شوید
تفسیر نتایج
در این شبیه سازی بازی تاس انداختن را 10000000 بار اجرا می کنیم تا درصد برد و باخت را مشاهده کنیم. با توجه به لبه خانه که قبلا محاسبه شده است (2%)، انتظار داریم که درصد ضرر کمی بیشتر از درصد برد باشد.
پس از اجرای شبیه سازی، ممکن است نتایجی مانند:
این نتایج کاملاً با احتمالات نظری (49٪ برد، 51٪ ضرر) مطابقت دارد، که نشان می دهد چگونه لبه خانه در تعداد زیادی آزمایش ظاهر می شود. عدم تعادل جزئی سودآوری کازینو را در دراز مدت تضمین می کند.
تجسم بردهای کوتاه مدت و باخت های بلند مدت
شبیهسازیهای مونت کارلو برای مدلسازی و پیشبینی نتایج از طریق نمونهگیری تصادفی مکرر قدرتمند هستند. در زمینه قمار، ما می توانیم از شبیه سازی مونت کارلو برای درک نتایج بالقوه استراتژی های شرط بندی مختلف استفاده کنیم.
ما یک شرطبند را شبیهسازی میکنیم که شرط اولیه یکسانی را در هر دور میگذارد و مشاهده میکنیم که چگونه ارزش حساب آنها در تعداد مشخصی از شرطبندیها تغییر میکند.
در اینجا نحوه شبیه سازی و تجسم سفر شرط بندی با استفاده از Matplotlib آمده است:
def bettor_simulation(funds, initial_wager, wager_count):
value = funds
wager = initial_wager
# Lists to store wager count and account value
wX = []
vY = []
current_wager = 1
while current_wager
وارد حالت تمام صفحه شوید
از حالت تمام صفحه خارج شوید
این نمودار نشان می دهد که چگونه ارزش حساب شرط بندی می تواند در طول زمان به دلیل برد و باخت نوسان کند. در ابتدا ممکن است دورههایی برای برنده شدن وجود داشته باشد (خط سبز بالاتر از مقدار شروع)، اما با افزایش تعداد شرطبندیها، اثر تجمعی لبه خانه آشکار میشود. در نهایت، ارزش حساب شرطگذار به سمت وجوه اولیه یا کمتر از آن (خط خاکستری) کاهش مییابد که نشاندهنده ضررهای بلندمدت است.
نتیجه
درک ریاضیات پشت سود کازینو، مزیت آشکاری را برای خانه در هر بازی از طریق مفهوم لبه خانه آشکار می کند. با وجود بردهای گاه به گاه، احتمالی که در بازیهای کازینو وجود دارد، تضمین میکند که بیشتر بازیکنان در طول زمان پول از دست خواهند داد. شبیهسازیهای مونت کارلو به وضوح این پویاییها را نشان میدهد و نشان میدهد که چگونه حتی بردهای کوتاهمدت میتوانند ضررهای بلندمدت را به دلیل مزیت آماری کازینو پنهان کنند. این بینش در مورد اطمینان ریاضی سودآوری کازینو بر اهمیت تصمیم گیری آگاهانه و شیوه های قمار مسئولانه تأکید می کند.
در مرحله بعد، میتوانیم تجسمها یا تغییرات اضافی را بررسی کنیم، مانند مقایسه استراتژیهای شرطبندی مختلف یا تجزیه و تحلیل تأثیر متغیر شرطبندیهای اولیه بر نتایج شرطبند.
در ارتباط باش:
از به اشتراک گذاشتن افکار، پرسیدن سؤالات و مشارکت در بحث دریغ نکنید.
کد نویسی مبارک!
آیا تا به حال فکر کرده اید که چرا کازینوها همیشه برنده می شوند؟ که در “شکست دادن شانس: ریاضیات پشت سود کازینوما ریاضیات ساده و استراتژیهای هوشمندانهای را بررسی میکنیم که تضمین میکند کازینوها در بلندمدت درآمد کسب میکنند. از طریق مثالهای قابل درک و شبیهسازیهای مونت کارلو، اسرار پشت لبه خانه را فاش خواهیم کرد. برای کشف اینکه چگونه کازینوها شانس را به نفع خود تغییر می دهند آماده شوید!
درک لبه خانه
لبه خانه یک مفهوم اساسی در دنیای کازینوها است. این نشان دهنده میانگین سودی است که کازینو انتظار دارد از هر شرط بندی بازیکنان به دست آورد. اساسا، این درصدی از هر شرط است که کازینو در دراز مدت حفظ می کند.
لبه خانه وجود دارد زیرا کازینوها شرط های برنده را بر اساس “شانس واقعی” بازی پرداخت نمی کنند. شانس واقعی نشان دهنده احتمال واقعی وقوع یک رویداد است. کازینوها با پرداخت با شانس کمی کمتر، مطمئن می شوند که در طول زمان سود می کنند.
لبه خانه (HE) به عنوان سود کازینو که به عنوان درصدی از شرط اولیه بازیکن بیان می شود، تعریف می شود.
** رولت اروپایی ** فقط یک صفر سبز دارد که در مجموع 37 عدد به آن می دهد. اگر بازیکنی 1 دلار روی قرمز شرط بندی کند، شانس 18/37 برنده شدن 1 دلار و 19/37 شانس باخت 1 دلار را دارد. مقدار مورد انتظار:
ارزش مورد انتظار=( 1 × 37/18
از این رو، در رولت اروپایی لبه خانه (HE) در اطراف است 2.7 درصد
بیایید بازی را برای خودمان بسازیم تا آن را بیشتر درک کنیم، بازی تاس انداختن ساده.
import random
def roll_dice():
roll = random.randint(1, 100)
if roll == 100:
print(roll, 'You rolled a 100 and lost. Better luck next time!')
return False
elif roll
در این بازی:
-
بازیکن 1/100 شانس باخت دارد اگر رول 100 باشد.
-
اگر بازی بین 1 تا 50 باشد، بازیکن 50/100 شانس باخت دارد.
-
اگر بازی بین 51 تا 99 باشد، بازیکن 49/100 شانس برنده شدن دارد.
مقدار مورد انتظار =(1×49/100) + (-1×51/100) = 49/100 − 51/100= −2/100 ≈ −2%
بنابراین، لبه خانه است 2 درصد
آشنایی با شبیه سازی مونت کارلو
شبیهسازی مونت کارلو ابزاری قدرتمند برای درک و پیشبینی سیستمهای پیچیده با اجرای شبیهسازیهای متعدد از یک فرآیند و مشاهده نتایج است. در زمینه کازینوها، شبیهسازیهای مونت کارلو میتوانند سناریوهای مختلف شرطبندی را مدلسازی کنند تا نشان دهند که چگونه لبه خانه سودآوری بلندمدت را تضمین میکند. بیایید بررسی کنیم که شبیهسازیهای مونت کارلو چگونه کار میکنند و چگونه میتوان آنها را در یک بازی ساده کازینو اعمال کرد.
شبیه سازی مونت کارلو چیست؟
شبیه سازی مونت کارلو شامل تولید متغیرهای تصادفی برای شبیه سازی یک فرآیند چندین بار و تجزیه و تحلیل نتایج است. با انجام هزاران یا حتی میلیونها تکرار، میتوانیم توزیعی از نتایج احتمالی را به دست آوریم و بینشی در مورد احتمال وقوع رویدادهای مختلف به دست آوریم.
استفاده از شبیه سازی مونت کارلو در بازی تاس انداختن
ما از شبیه سازی مونت کارلو برای مدل سازی بازی تاس انداختن که قبلا در مورد آن صحبت کردیم استفاده خواهیم کرد. این به ما کمک می کند بفهمیم که چگونه لبه خانه بر سودآوری بازی در طول زمان تأثیر می گذارد.
`def monte_carlo_simulation(trials):
wins = 0
losses = 0
for _ in range(trials):
if roll_dice():
wins += 1
else:
losses += 1
win_percentage = (wins / trials) * 100
loss_percentage = (losses / trials) * 100
houseEdge= loss_percentage-win_percentage
print(f"After {trials} trials:")
print(f"Win percentage: {win_percentage:.2f}%")
print(f"Loss percentage: {loss_percentage:.2f}%")
print(f"House Edge: {houseEdge:.2f}%")
# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`
تفسیر نتایج
در این شبیه سازی بازی تاس انداختن را 10000000 بار اجرا می کنیم تا درصد برد و باخت را مشاهده کنیم. با توجه به لبه خانه که قبلا محاسبه شده است (2%)، انتظار داریم که درصد ضرر کمی بیشتر از درصد برد باشد.
پس از اجرای شبیه سازی، ممکن است نتایجی مانند:
این نتایج کاملاً با احتمالات نظری (49٪ برد، 51٪ ضرر) مطابقت دارد، که نشان می دهد چگونه لبه خانه در تعداد زیادی آزمایش ظاهر می شود. عدم تعادل جزئی سودآوری کازینو را در دراز مدت تضمین می کند.
تجسم بردهای کوتاه مدت و باخت های بلند مدت
شبیهسازیهای مونت کارلو برای مدلسازی و پیشبینی نتایج از طریق نمونهگیری تصادفی مکرر قدرتمند هستند. در زمینه قمار، ما می توانیم از شبیه سازی مونت کارلو برای درک نتایج بالقوه استراتژی های شرط بندی مختلف استفاده کنیم.
ما یک شرطبند را شبیهسازی میکنیم که شرط اولیه یکسانی را در هر دور میگذارد و مشاهده میکنیم که چگونه ارزش حساب آنها در تعداد مشخصی از شرطبندیها تغییر میکند.
در اینجا نحوه شبیه سازی و تجسم سفر شرط بندی با استفاده از Matplotlib آمده است:
def bettor_simulation(funds, initial_wager, wager_count):
value = funds
wager = initial_wager
# Lists to store wager count and account value
wX = []
vY = []
current_wager = 1
while current_wager
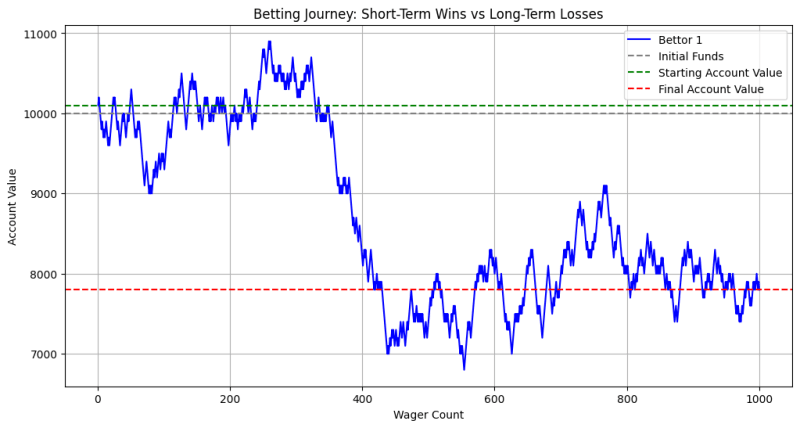
این نمودار نشان می دهد که چگونه ارزش حساب شرط بندی می تواند در طول زمان به دلیل برد و باخت نوسان کند. در ابتدا ممکن است دورههایی برای برنده شدن وجود داشته باشد (خط سبز بالاتر از مقدار شروع)، اما با افزایش تعداد شرطبندیها، اثر تجمعی لبه خانه آشکار میشود. در نهایت، ارزش حساب شرطگذار به سمت وجوه اولیه یا کمتر از آن (خط خاکستری) کاهش مییابد که نشاندهنده ضررهای بلندمدت است.
نتیجه
درک ریاضیات پشت سود کازینو، مزیت آشکاری را برای خانه در هر بازی از طریق مفهوم لبه خانه آشکار می کند. با وجود بردهای گاه به گاه، احتمالی که در بازیهای کازینو وجود دارد، تضمین میکند که بیشتر بازیکنان در طول زمان پول از دست خواهند داد. شبیهسازیهای مونت کارلو به وضوح این پویاییها را نشان میدهد و نشان میدهد که چگونه حتی بردهای کوتاهمدت میتوانند ضررهای بلندمدت را به دلیل مزیت آماری کازینو پنهان کنند. این بینش در مورد اطمینان ریاضی سودآوری کازینو بر اهمیت تصمیم گیری آگاهانه و شیوه های قمار مسئولانه تأکید می کند.
در مرحله بعد، میتوانیم تجسمها یا تغییرات اضافی را بررسی کنیم، مانند مقایسه استراتژیهای شرطبندی مختلف یا تجزیه و تحلیل تأثیر متغیر شرطبندیهای اولیه بر نتایج شرطبند.
در ارتباط باش:
از به اشتراک گذاشتن افکار، پرسیدن سؤالات و مشارکت در بحث دریغ نکنید.
کد نویسی مبارک!