قدرت نمودارها: از تجزیه و تحلیل شبکه های اجتماعی گرفته تا ردیابی بیماری

آیا هرگز تعجب کرده اید که فیس بوک چگونه می داند دوستان متقابل شما چه کسانی هستند ، یا چگونه Google Maps سریعترین مسیر را از طریق پیچ و خم خیابان ها پیدا می کند؟ این راز در دنیای ظریف و شگفت آور قدرتمند نمودارها نهفته است – راهی برای دیدن ارتباطات که همه چیز را از زندگی اجتماعی به مبارزه با همه گیر تبدیل می کند.
در دنیای متصل تر امروز ، روابط و ارتباطات همه چیز است. از شبکه اجتماعی تعامل گرفته تا مسیرهای پیچیده انتقال بیماری و کارآمدترین مسیرهای سفر روزانه ما ، الگوهای وجود دارد که با مطالعه نمودارها به بهترین وجه قابل توضیح است. این وبلاگ به بررسی قلمرو جالب نظریه گراف ، مفاهیم اساسی آن ، بازنمودهای مختلف در علوم کامپیوتر و برنامه های تأثیرگذار آن در زمینه های مختلف می پردازد.
آشنایی با نمودارها
اساساً ، یک نمودار یک شیء ریاضی است که برای توصیف روابط بین اشیاء استفاده می شود. این ساخته شده است:
گره ها (یا رئوس): این اشیاء یا موجودات موجود در سیستم ما هستند. افراد را در یک شبکه اجتماعی ، شهرها روی نقشه یا ژن ها در یک مسیر بیولوژیکی در نظر بگیرید.
لبه ها: این روابط یا پیوندها بین گره ها است. اینها ممکن است دوستی ، جاده هایی باشد که به شهرها پیوند می دهند یا تعامل پروتئین پروتئین.
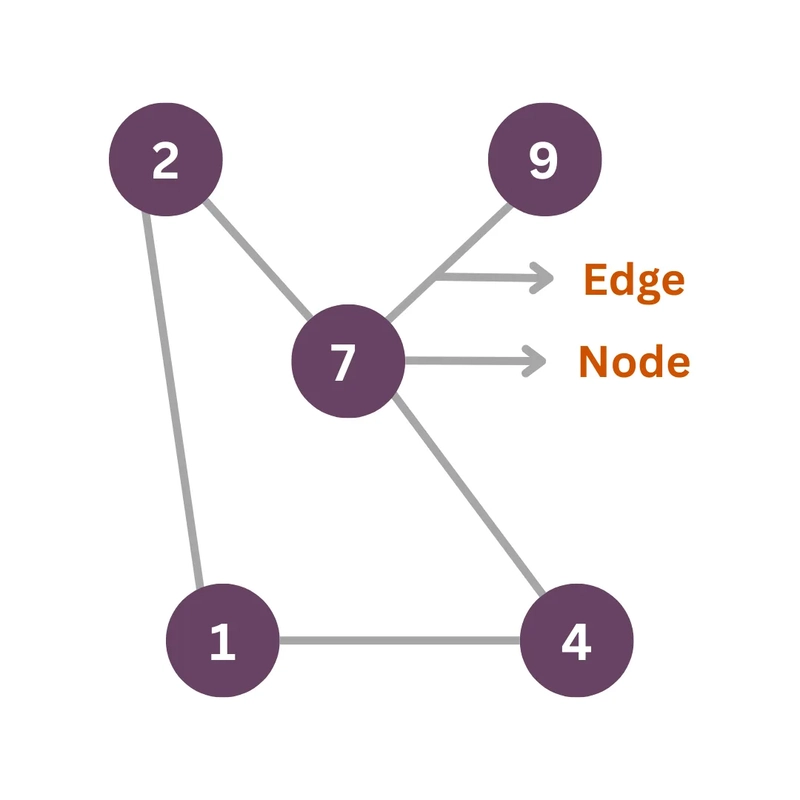
نمودار: چشم انداز DSA
از دیدگاه ساختار داده ها و الگوریتم های (DSA) ، نمایندگی و کار با نمودارها به طور مؤثر مهم است. چندین نمایندگی محبوب وجود دارد که هر کدام بسته به این عملکرد عملکرد خود را در مقابل تجارت فضا دارند.
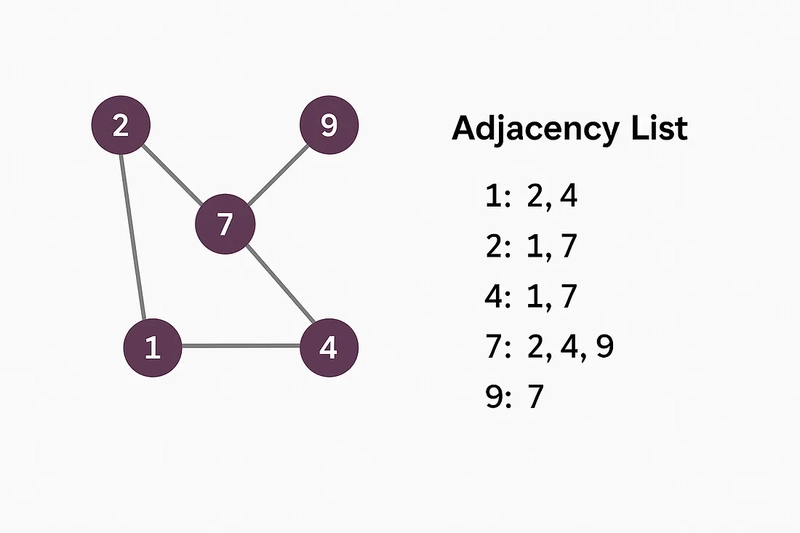
لیست مجاورت
نمایندگی: یک لیست مجاور ، نمودار را به عنوان یک آرایه (یا نقشه هش) از لیست ها نشان می دهد. شاخص آرایه یک گره را نشان می دهد ، و لیست در آن شاخص شامل تمام گره هایی است که مستقیماً با گره فعلی (همسایگان آن) مرتبط هستند.
class GraphAdjList:
def __init__(self, num_vertices):
self.num_vertices = num_vertices
self.adj_list = [[] for _ in range(num_vertices)]
def add_edge(self, u, v):
self.adj_list[u].append(v)
self.adj_list[v].append(u) # For an undirected graph
def __str__(self):
representation = ""
for i in range(self.num_vertices):
representation += f"{i}: {self.adj_list[i]}\n"
return representation
# Example usage
g_adj_list = GraphAdjList(5)
g_adj_list.add_edge(0, 1)
g_adj_list.add_edge(0, 4)
g_adj_list.add_edge(1, 2)
g_adj_list.add_edge(1, 3)
g_adj_list.add_edge(1, 4)
g_adj_list.add_edge(2, 3)
g_adj_list.add_edge(3, 4)
print(g_adj_list)
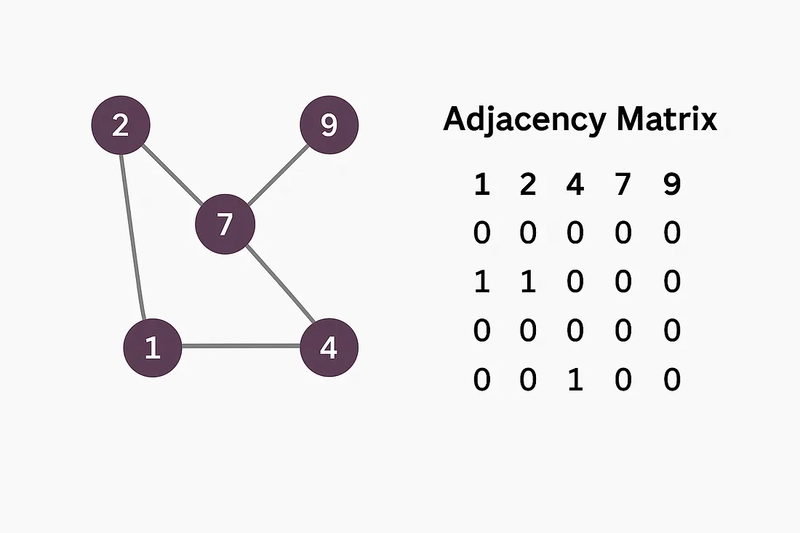
ماتریس مجاورت
نمایندگی: یک ماتریس مجاور یک آرایه 2D (یا ماتریس) است که در آن هر دو ردیف و ستون گره های نمودار را نشان می دهند. ورودی در ماتریس[i][j] به طور معمول 1 (یا درست) اگر لبه ای بین گره I و گره J و 0 (یا کاذب) وجود داشته باشد. برای نمودارهای وزنی ، وزن لبه به جای 1 قابل ذخیره است.
class GraphAdjMatrix:
def __init__(self, num_vertices):
self.num_vertices = num_vertices
self.adj_matrix = [[0] * num_vertices for _ in range(num_vertices)]
def add_edge(self, u, v):
self.adj_matrix[u][v] = 1
self.adj_matrix[v][u] = 1 # For an undirected graph
def __str__(self):
representation = ""
for row in self.adj_matrix:
representation += f"{row}\n"
return representation
# Example usage
g_adj_matrix = GraphAdjMatrix(5)
g_adj_matrix.add_edge(0, 1)
g_adj_matrix.add_edge(0, 4)
g_adj_matrix.add_edge(1, 2)
g_adj_matrix.add_edge(1, 3)
g_adj_matrix.add_edge(1, 4)
g_adj_matrix.add_edge(2, 3)
g_adj_matrix.add_edge(3, 4)
print(g_adj_matrix)
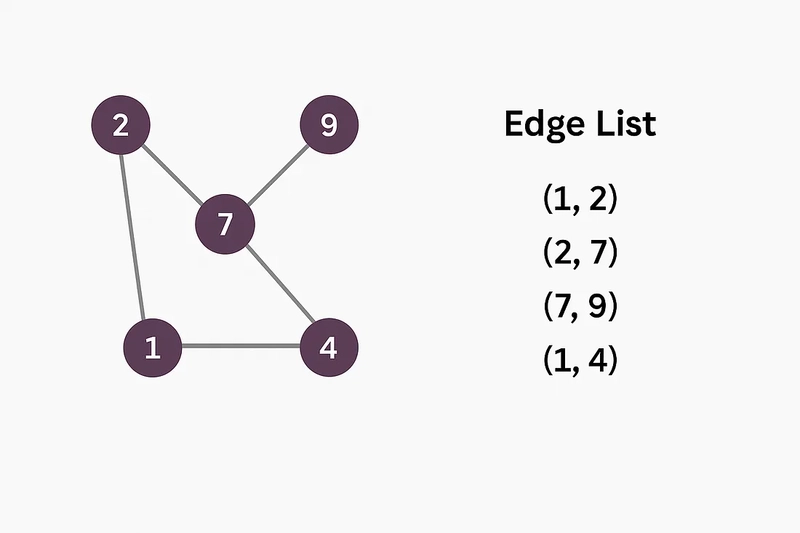
لیست لبه
نمایندگی: یک لیست Edge یک نمایش اساسی است که لیستی از تمام لبه های موجود در نمودار را در خود نگه می دارد. هر ورودی در لیست معمولاً لبه ای را به عنوان یک جفت گره ای که در آن وصل می شود توصیف می کند. در نمودارهای وزنی ، وزن ممکن است به عنوان یک مورد سوم در Tuple اضافه شود.
class GraphEdgeList:
def __init__(self):
self.edges = []
def add_edge(self, u, v):
self.edges.append((u, v))
def __str__(self):
return f"Edges: {self.edges}"
# Example usage
g_edge_list = GraphEdgeList()
g_edge_list.add_edge(0, 1)
g_edge_list.add_edge(0, 4)
g_edge_list.add_edge(1, 2)
g_edge_list.add_edge(1, 3)
g_edge_list.add_edge(1, 4)
g_edge_list.add_edge(2, 3)
g_edge_list.add_edge(3, 4)
print(g_edge_list)
همانطور که قبلاً ذکر شد ، ماتریس مجاور در واقع یک ماتریس 2D است. ارزش آن را دارد که سودمندی آن را برای برخی از عملیات نمودار تکرار کنید ، مانند تأیید حضور یک لبه بین دو گره در زمان ثابت. اما برای نمودارهای پراکنده (نمودارهایی با لبه های بسیار کمتری نسبت به حداکثر تعداد ممکن) ، ماتریس مجاور از نظر حافظه می تواند بی فایده باشد.
برنامه
قدرت نمودارها در استفاده چند جانبه آنها در مناطق مختلف نهفته است.
1. تجزیه و تحلیل شبکه های اجتماعی
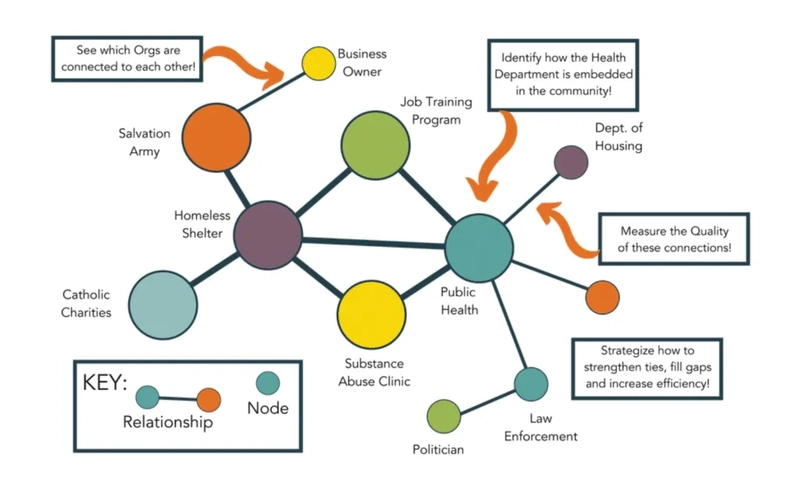
شبکه های اجتماعی مانند Facebook ، Twitter و LinkedIn به عنوان گره ها و دوستی ها (دنبال یا پیام) به عنوان لبه ها نمودارهای عظیمی هستند. الگوریتم های نمودار برای:
تأثیرگذار را پیدا کنید: استفاده از اقدامات مرکزیت مانند PageRank (مشهور توسط Google برای رتبه بندی صفحه وب بر اساس ساختار پیوند) یا مرکزیت بین (محاسبه چند بار یک گره در کوتاهترین مسیر بین گره های دیگر) ، می توانیم با تأثیرگذارترین افراد در یک شبکه پیدا کنیم.
تشخیص جامعه: روش هایی مانند Girvan-Newman (لبه هایی را با بیشترین میزان مرکزیت تکراری) یا روش لووین (یک الگوریتم حریص که به طور تکراری مدولار را پیدا می کند) در تشخیص خوشه ها یا جوامع در یک شبکه کمک می کند ، و گروه هایی از کاربران را با اتصالات دچار ایجاد می کند.
سیستم های توصیه: با محاسبه تعامل کاربر به عنوان نمودار ، سایت ها می توانند دوستان ، گروه ها یا محتوا را بر اساس فعالیت ها و ارتباطات کاربران مجاور توصیه کنند. این از این واقعیت استفاده می کند که کاربران متصل تمایل به داشتن علایق مشابه دارند.
2. ردیابی بیماری و مدل سازی اپیدمی
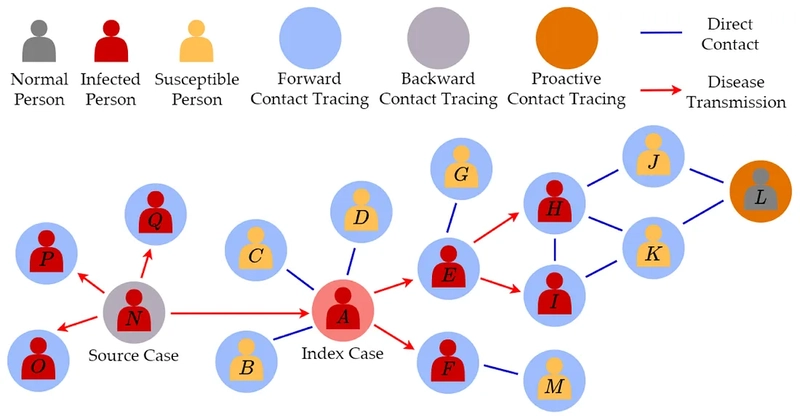
نمودارها در مدل سازی گسترش بیماری ضروری هستند. به عنوان مثال:
ردیابی تماس: در شیوع COVID-19 ، از نمودارها برای مدل سازی شبکه های تماس استفاده شده است که در آن گره ها افراد هستند و لبه ها تعامل هستند. از الگوریتم های جستجوی وسعت اول (BFS) برای یافتن همه افرادی که با یک فرد آلوده تعامل داشتند ، استفاده شد و این امکان را برای انجام کارآمد ردیابی تماس فراهم می کند.
آستانه همه گیر: از طریق مدل های مبتنی بر نمودار ، دانشمندان می توانند در مورد سرعتی که یک بیماری با استفاده از پیکربندی شبکه و ویژگی هایی مانند میانگین تعداد مخاطبین برای یک فرد گسترش می یابد ، پیش بینی کنند. این آستانه بحرانی مصونیت گله را آگاه می کند و برای هدایت مداخلات بهداشت عمومی استفاده می شود.
3. حمل و نقل و مسیریابی
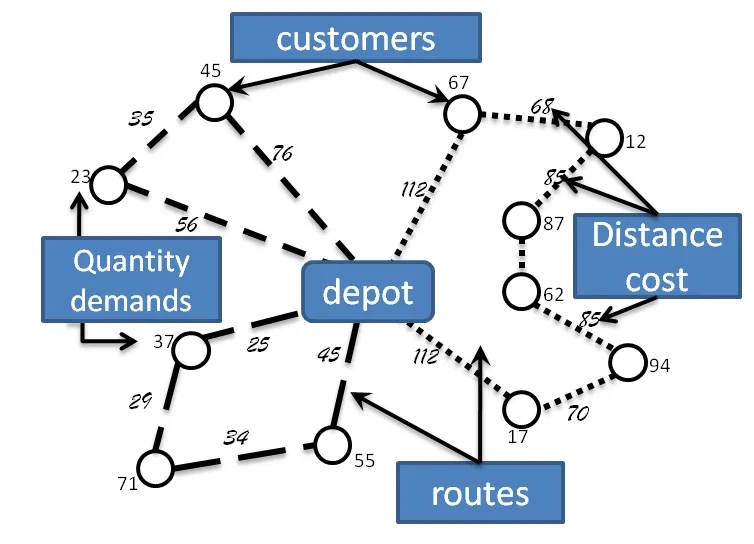
الگوریتم های نمودار ، سیستم های ناوبری نقشه مانند Google Maps را تشکیل می دهند. به عنوان مثال:
الگوریتم های کوتاهترین مسیر: از الگوریتم های Dijkstra و A* برای تعیین سریعترین یا کوتاهترین مسیر بین دو نقطه استفاده می شود و با در نظر گرفتن عواملی مانند زمان سفر و مسافت در نظر گرفته می شود.
بهینه سازی ترافیک: با نمایندگی از شهرها به عنوان نمودارها ، تقاطع ها به عنوان گره و جاده ها به عنوان لبه ها (احتمالاً در سطح ترافیک وزن دارند) ، می توان ترافیک را برای کاهش احتقان و افزایش راندمان مدل سازی و بهینه کرد.
الگوریتم های نمودار در عمل
برخی از الگوریتم های نمودار اصلی این موارد را هدایت می کنند:
1. جستجوی وسعت اول (BFS): سطح نمودار را بر اساس سطح می گذرد.
- اعمال شده در: شبکه های اجتماعی برای تعیین کوتاهترین مسیر (تعداد اتصالات) بین کاربران.
- مورد استفاده در: ردیابی بیماری برای یافتن همه افرادی که در تعدادی از مخاطبین با یک فرد آلوده در تماس بوده اند.
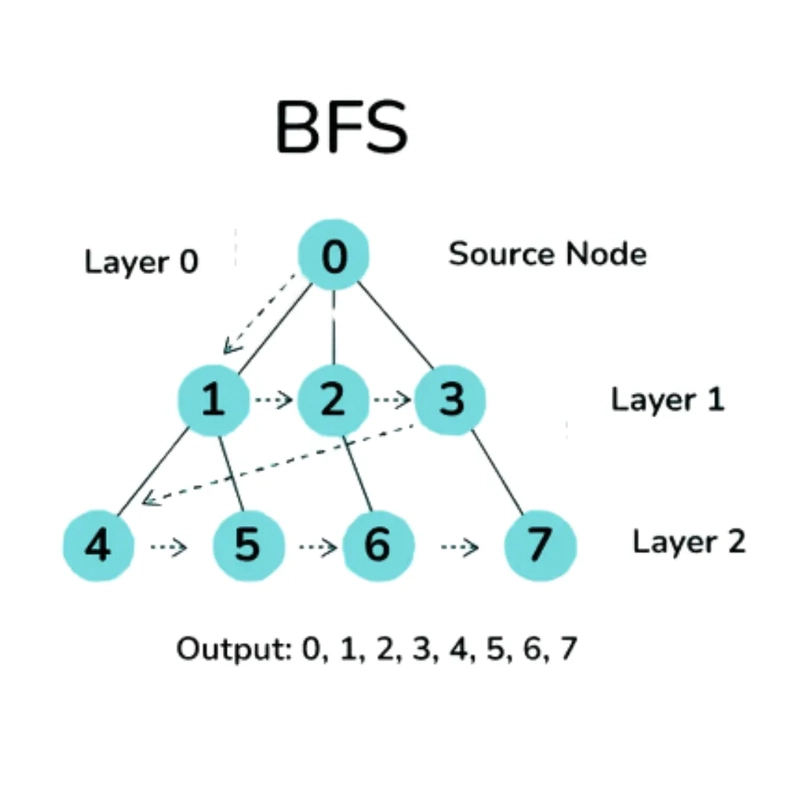
2. جستجوی عمق اول (DFS): تا حد امکان در طول هر شاخه قبل از بازگشت به عقب سفر می کند.
- کمک در تشخیص: چرخه در نمودارهای وابستگی ، به عنوان مثال ، پیش نیازهای دوره یا وابستگی های نرم افزاری (اگر چرخه ای وجود داشته باشد ، این بدان معنی است که وابستگی دایره ای وجود دارد).
- مورد استفاده در: بازی های پازل و الگوریتم های حل کننده پیچ و خم که در آن همه اکتشافات ممکن در خیابان مورد نیاز است.
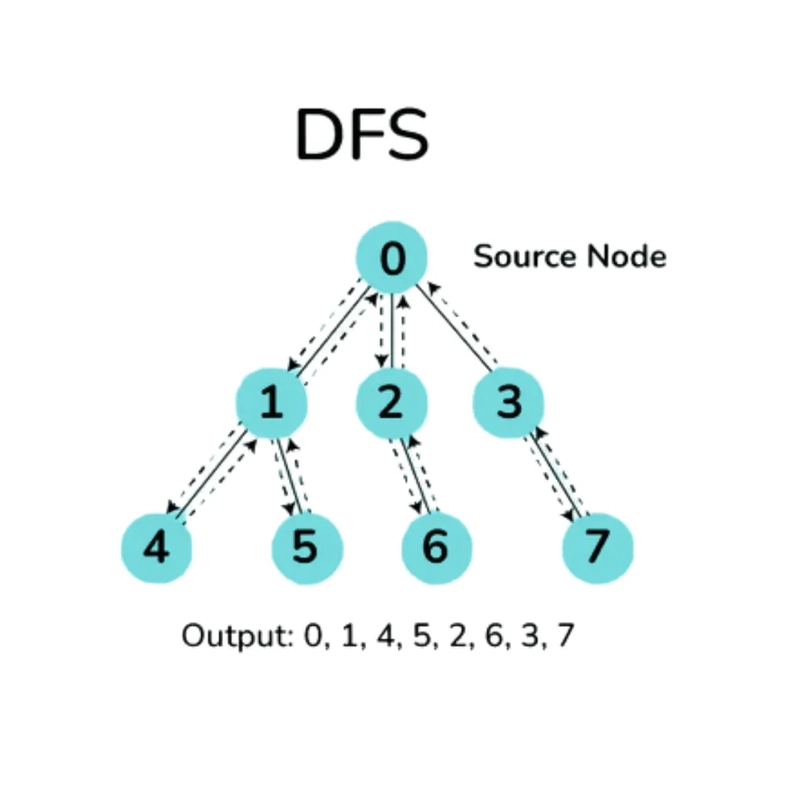
3. الگوریتم Dijkstra: کوتاهترین مسیر را از یک گره منبع به تمام گره های دیگر در یک نمودار با وزن لبه های غیر منفی تعیین می کند.
- قدرتها: سیستم های ناوبری از طریق یافتن کوتاهترین مسیرها.
- مورد استفاده در: الگوریتم های مسیریابی شبکه برای به حداقل رساندن تحویل بسته های داده با توجه به تأخیر یا هزینه شبکه.
4. الگوریتم Floyd-Warshall: کوتاهترین مسیرها را بین هر جفت گره در یک نمودار وزنی محاسبه می کند (از وزن لبه منفی پشتیبانی می کند ، اما چرخه های منفی نیست).
- مورد استفاده در: برنامه ریزی تحویل و تدارکات حمل و نقل برای یافتن بهترین مسیرها بین چندین مقصد ، بر اساس مسافت یا هزینه بین همه نقاط.
5. حداقل الگوریتم های درخت پوششی (MST) (به عنوان مثال ، Kruskal's ، Prim): زیر مجموعه ای از لبه ها را تعیین کنید که تمام راس ها را در یک ساختار درخت متصل می کند ، بدون چرخه و حداقل وزن لبه.
- اعمال شده در: ایجاد شبکه های مقرون به صرفه ، مانند شبکه های برقی ، سیستم های ارتباطات از راه دور یا تنظیمات کابل اینترنتی ، برای کاهش هزینه نصب اتصالات و هنوز هم هر نقطه مرتبط است.
آینده نمودارها
برنامه های تئوری نمودار با سرعت رعد و برق در حال گسترش هستند.
شبکه های عصبی نمودار (GNN): این زمینه در حال رشد ، تئوری نمودار و یادگیری ماشین را در یک ترکیب قدرتمند جمع می کند. GNN ها می توانند بازنمایی گره و نمودار را بدست آورند ، و بنابراین راه حل هایی برای مشکلات سخت مانند کشف مواد مخدر (پیش بینی تعامل مولکول) ، تشخیص کلاهبرداری (تشخیص الگوهای ناهنجار در نمودارهای معاملات مالی) و توصیه اجتماعی با بینش متنی بهبود یافته.
تجزیه و تحلیل شبکه در زمان واقعی: با حذف داده های شبکه های پویا مانند جریان رسانه های اجتماعی و معاملات مالی ، ایجاد الگوریتم های نمودار جریان جریان ضروری است. این الگوریتم ها می توانند در حال تغییر شبکه ها در زمان واقعی ، ردیابی به موقع روندها ، ناهنجاری ها و حوادث مهم را ردیابی و تجزیه و تحلیل کنند.
پایان
نمودارها روشی قوی و انعطاف پذیر برای درک و مدل سازی به هم پیوسته جهان ما هستند. از الگوریتم های پشت فیدهای رسانه های اجتماعی و سیستم های ناوبری ما گرفته تا مدل های مورد استفاده برای ردیابی و مبارزه با بیماری ها ، “قدرت نمودارها” قابل بحث نیست. هرچه اطلاعات پیچیده تر و یکپارچه تر می شوند ، تئوری نمودار و برنامه های الگوریتمی آن به طور فزاینده ای برای مقابله با اساسی ترین و آزار دهنده ترین چالش ها و رونمایی از فرصت های جدید در طیف گسترده ای از زمینه ها ارزشمند می شوند.



